��Ŀ����
����Ŀ����ͼ���ı���![]() ��ij������һ�߳�Ϊ
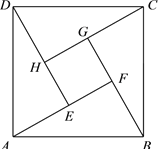
��ij������һ�߳�Ϊ![]() ���������εؿ��ƽ��ʾ��ͼ. �ּƻ��ڸõؿ��ϻ����ĸ���ȫ��ͬ��ֱ�������Σ���
���������εؿ��ƽ��ʾ��ͼ. �ּƻ��ڸõؿ��ϻ����ĸ���ȫ��ͬ��ֱ�������Σ���![]() ��
��![]() �����������ĸ�ֱ�������������ڽ����̻����м��С�����������������㳡��Ϊ�˷������。���㳡������
�����������ĸ�ֱ�������������ڽ����̻����м��С�����������������㳡��Ϊ�˷������。���㳡������![]() ��·
��·![]()
![]()
![]()
![]() . ��֪��ֱ���������ڽ����̻�ÿ1��ƽ���ķ���Ϊ
. ��֪��ֱ���������ڽ����̻�ÿ1��ƽ���ķ���Ϊ![]() Ԫ���м�С���������㳡ÿ1��ƽ���ķ���Ϊ
Ԫ���м�С���������㳡ÿ1��ƽ���ķ���Ϊ![]() Ԫ����·ÿ1���ķ���Ϊ
Ԫ����·ÿ1���ķ���Ϊ![]() Ԫ������
Ԫ������![]() Ϊ����������
����������![]() ��
��![]() .
.
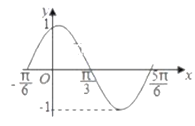
��1����![]() ��ʾ�ù��̵������
��ʾ�ù��̵������![]() ��
��
��2����![]() Ϊ��ֵʱ���ù��̵��������ͣ�
Ϊ��ֵʱ���ù��̵��������ͣ�
���𰸡���1��![]() ��
��![]() ����2����
����2����![]() ʱ��
ʱ��![]() ȡ����Сֵ
ȡ����Сֵ
��������
(1)���������֪![]() ,
,![]() ,�������
,�������![]() ��
��![]() ����������
����������![]() ����.
����.
(2)��(1)��![]() ,�����������ĵ���������ֵ����.
,�����������ĵ���������ֵ����.
��1����![]() ��,
��,![]() ,
,![]() ,����
,����![]() ,
,![]() .
.
����![]() ��
��![]() ���ĸ���ȫ��ͬ��ֱ��������,����
���ĸ���ȫ��ͬ��ֱ��������,����![]() ,
,![]() ,
,
����![]() ,
,
![]() .
.
����![]()
![]()
![]() ,
,![]() .
.
��2���ɣ�1����![]() ,
,![]() .
.
��![]() .
.
��![]() ,��Ϊ
,��Ϊ![]() ,����
,����![]() ��
��![]() (��).
(��).
��![]() ,���Ե�
,���Ե�![]() ʱ,
ʱ,![]() ,
,![]() �����ݼ���
�����ݼ���
��![]() ʱ,
ʱ,![]() ,
,![]() ��������. ���Ե�
��������. ���Ե�![]() ʱ,
ʱ,![]() ȡ�ü�Сֵ,Ҳ����Сֵ,
ȡ�ü�Сֵ,Ҳ����Сֵ,
��![]() ,���Ե�
,���Ե�![]() ʱ,
ʱ,![]() ȡ����Сֵ.
ȡ����Сֵ.

��ϰ��ϵ�д�
 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д�
�����Ŀ