题目内容
【题目】已知圆C与圆C1:5x2+5y2﹣mx﹣16y+32=0外切于点P(![]() ),且与y轴相切.
),且与y轴相切.
(1)求圆C的方程
(2)过点O作直线l1,l2分别交圆C于A、B两点,若l1,l2斜率之积为﹣2,求△ABC面积S的最大值
【答案】(1)(x﹣1)2+y2=1;(2)![]() .
.
【解析】
(1)根据P(![]() )在圆C1上,有
)在圆C1上,有![]() ,求得m=22,得
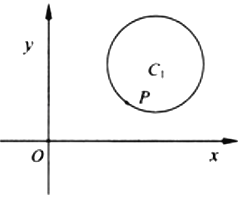
,求得m=22,得![]() ,C1P方程为4x﹣3y﹣4=0,设C(x0,y0)(x0>0),根据圆C与y轴相切和圆C与圆C1外切于P,建立方程组
,C1P方程为4x﹣3y﹣4=0,设C(x0,y0)(x0>0),根据圆C与y轴相切和圆C与圆C1外切于P,建立方程组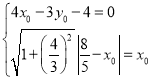 求解.
求解.
(2)根据题意设l1:y=kx,l2:y![]() x,由
x,由![]() ,消去y得(k2+1)x2+2x=0,解得x=0,
,消去y得(k2+1)x2+2x=0,解得x=0,![]() ,得到
,得到![]() ,同理可得
,同理可得 ,①当直线AB的斜率不存在时,易得
,①当直线AB的斜率不存在时,易得![]() ;②当直线AB的斜率存在时,直线AB的方程为
;②当直线AB的斜率存在时,直线AB的方程为![]() ,化简得
,化简得![]() ,直线AB恒过
,直线AB恒过![]() ,然后由
,然后由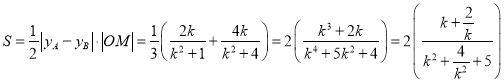 求解.
求解.
(1)∵P(![]() )在圆C1上,∴
)在圆C1上,∴![]() ,
,
解得m=22,
∴圆![]() ,得
,得![]() ,
,
可得C1P方程为4x﹣3y﹣4=0,
设C(x0,y0)(x0>0),
∵圆C与y轴相切,∴r=x0,
又圆C与圆C1外切于P,∴C在直线C1P上,且CP=r,
则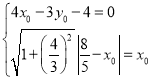 ,解得
,解得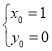 或
或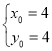 ,
,
∵圆C与圆C1外切,∴C(1,0),
∴圆C的方程为(x﹣1)2+y2=1;
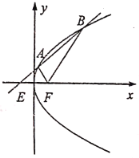
(2)如图所示:
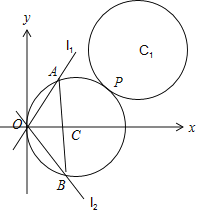
设直线l1的斜率为k(不妨设k>0),则直线l2的斜率为![]() ,
,
∴l1:y=kx,l2:y![]() x,
x,
由![]() ,消去y得(k2+1)x2+2x=0,
,消去y得(k2+1)x2+2x=0,
解得x=0,![]() ,∴
,∴![]() ,
,
以![]() 代k同理可得
代k同理可得 ,
,
①当直线AB的斜率不存在时,
由![]() ,得
,得![]() ,弦AB的长度为
,弦AB的长度为![]() ,
,![]() ;
;
②当直线AB的斜率存在时,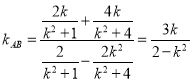 ,
,
∴直线AB的方程为![]() ,化简得
,化简得![]() ,
,
∴直线AB恒过![]() ,
,
∴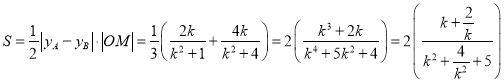 .
.
设![]() ,则
,则![]() ,
,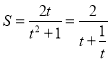 ,
,
设![]() ,
,![]() ,
,
∴f(t)在![]() 上单调增,得
上单调增,得![]() ,
,
∴![]() .
.
综上,△ABC面积S的最大值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目