题目内容
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,记
,记![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且数列
,且数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)① 计算![]() ,
,![]() 的值;
的值;
② 猜想![]() ,
,![]() 满足的关系式,并用数学归纳法加以证明;
满足的关系式,并用数学归纳法加以证明;
(2)若数列![]() 通项公式为
通项公式为![]() ,证明:
,证明:![]() .
.![]()
【答案】(1)①![]() ,
,![]() ;②
;②![]() ,证明见解析;(2)见解析
,证明见解析;(2)见解析
【解析】
(1)①根据题中给的递推公式直接计算![]() ,
,![]() 即可.
即可.
②由①中可知![]() ,
,![]() ,故猜想
,故猜想![]() ,再根据数学归纳法的方法证明即可.
,再根据数学归纳法的方法证明即可.
(2)根据![]() 可求得
可求得![]() ,再利用(1)中的结论放缩可得
,再利用(1)中的结论放缩可得![]() ,再构造函数
,再构造函数![]() 证明其单调性,再累加证明
证明其单调性,再累加证明![]() 即可.
即可.
(1)①![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
② ![]()
![]() .
.
猜想:![]() . (也可以写成
. (也可以写成![]() )
)
1°当![]() 时,
时,![]() 成立;
成立;
2°假设当![]() 时,
时,![]() 成立,
成立,
当![]() 时,
时,![]() .
.
综上1°,2°所述,![]() .
.
(2)因![]() ,所以其前
,所以其前![]() 项和
项和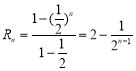 .
.
所以由(1)知![]() .
.
令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,所以
,所以![]() .令
.令![]() ,所以
,所以![]() ,
,
即![]() ,
,
即![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ,
,![]() ,……,
,……,![]() ,
,
上述![]() 个式子相加,得
个式子相加,得![]() ,
,
所以![]() ,则
,则![]() ,即
,即![]() ,故
,故![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】随着夏季的到来,冰枕成为市面上的一种热销产品,某厂家为了调查冰枕在当地大学的销售情况,作出调研,并将所得数据统计如下表所示:
表一:
温度在30℃以下 | 温度在30℃以上 | 总计 | |
女生 | 10 | 30 | 40 |
男生 | 40 | 20 | 60 |
总计 | 50 | 50 | 100 |
随后在该大学一个小卖部调查了冰枕的出售情况,并将某月的日销售件数(x)与销售天数(y)统计如下表所示:
表二:
第 | 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)请根据表二中的数据在下列网格纸中绘制散点图;
(2)请根据表二中提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)从(1)(2)中的数据及回归方程我们可以得到,销售件数随着销售天数的增长而增长,但无法判断男、女生对冰枕的选择是否与温度有关,请结合表一中的数据,并自己设计方案来判段是否有99.9%的可能性说明购买冰枕的性别与温度相关.
参考数据及公式:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
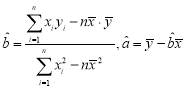 ;
;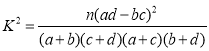 ,其中
,其中![]() .
.
【题目】某产品的三个质量指标可用有序实数对![]() 表示,用综合指标
表示,用综合指标![]() 评价该产品的等级.若
评价该产品的等级.若![]() ,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号 |
|
|
|
|
|
产品指标 |
|
|
|
|
|
产品编号 |
|
|
|
|
|
产品指标 |
|
|
|
|
|
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品的一等品中,随机抽取2件产品,设事件![]() 为“在取出的2件产品中,每件产品的综合指标
为“在取出的2件产品中,每件产品的综合指标![]() 都等于4”,求事件
都等于4”,求事件![]() 发生的概率.
发生的概率.