题目内容
记函数f(x)=
的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域为B,求
(1)A,B;
(2)若B⊆A,求实数a的取值范围.
|
(1)A,B;
(2)若B⊆A,求实数a的取值范围.
(1)
≥0,等价于
即x<-1或x≥1
∴A=(-∞,-1)∪[1,+∞)
由(x-a-1)(2a-x)>0,得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a,∴B=(2a,a+1).
(2)∵B⊆A,∴2a≥1或a+1≤-1,即a≥
或a≤-2,而a<1,
∴
≤a<1或a≤-2,
故当B⊆A时,实数a的取值范围是(-∞,-2]∪[
,1)
| x-1 |
| x+1 |
|
∴A=(-∞,-1)∪[1,+∞)
由(x-a-1)(2a-x)>0,得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a,∴B=(2a,a+1).
(2)∵B⊆A,∴2a≥1或a+1≤-1,即a≥
| 1 |
| 2 |
∴
| 1 |
| 2 |
故当B⊆A时,实数a的取值范围是(-∞,-2]∪[
| 1 |
| 2 |

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
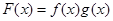 是R上的奇函数,当
是R上的奇函数,当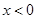 时,
时,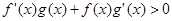 ,且
,且 ,则不等式
,则不等式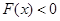 的解集是( )
的解集是( )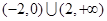
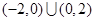
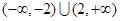
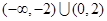
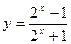 的值域是
的值域是 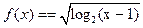 的定义域为A,集合
的定义域为A,集合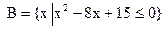 ,
,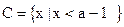 (1)求
(1)求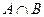 ; (2)若
; (2)若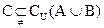 ,求
,求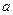 的取值范围。
的取值范围。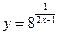 的定义域是______;值域是______.
的定义域是______;值域是______.