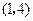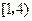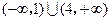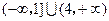题目内容
选修4-5:不等式选讲:
设函数f(x)=
(a∈R).
(1)当a=1时,求函数f(x)的定义域;
(2)若函数f(x)的定义域为R,试求a的取值范围.
设函数f(x)=
| |ax-2|+|ax-a|-2 |
(1)当a=1时,求函数f(x)的定义域;
(2)若函数f(x)的定义域为R,试求a的取值范围.
(1)由题设知:|x-2|+|x-1|-2≥0等价于:
⇒x≤
,
或
⇒x∈∅,
或
⇒x≥
,
综上所述,当a=1时,函数f(x)的定义域为(-∞,
]∪[
,+∞).
(2)由题设知,当x∈R时,恒有|ax-2|+|ax-a|-2≥0,
即|ax-2|+|ax-a|≥2恒成立,
∵|ax-2|+|ax-a|≥|(ax-2)-(ax-a)|=|a-2|,
∴只需|a-2|≥2,
解得a≤0,或a≥4.
|
| 1 |
| 2 |
或
|
或
|
| 5 |
| 2 |
综上所述,当a=1时,函数f(x)的定义域为(-∞,
| 1 |
| 2 |
| 5 |
| 2 |
(2)由题设知,当x∈R时,恒有|ax-2|+|ax-a|-2≥0,
即|ax-2|+|ax-a|≥2恒成立,
∵|ax-2|+|ax-a|≥|(ax-2)-(ax-a)|=|a-2|,
∴只需|a-2|≥2,
解得a≤0,或a≥4.

练习册系列答案
相关题目
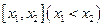 的长度为
的长度为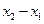 .已知函数
.已知函数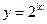 的定义域为
的定义域为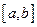 ,值域为
,值域为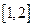 ,则区间
,则区间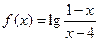 的定义域为( )
的定义域为( )