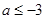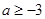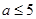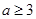题目内容
已知f(
)=2(
),
(1)求函数f(x)的解析式;
(2)求函数f(x)在区间[
,3]上的值域.
| 1+x |
| 1-x |
| 1+x2 |
| 1-x2 |
(1)求函数f(x)的解析式;
(2)求函数f(x)在区间[
| 1 |
| 2 |
(1)令t=
(t≠-1),则x=
.
∴
=
=
=
(t+
).
f(t)=2×
(t+
)=t+
(t≠-1).
即f(x)=x+
(x≠-1).
(2)∵f′(x)=1-
=
(x≠-1).令f′(x)=0,解得x=1.
在区间[
,1)上f′(x)<0,函数f(x)单调递减;在区间(1,3]上f′(x)>0,函数f(x)单调递增.
f(x)min=f(1)=2,
而f(
)=
,f(3)=
,∴f(x)max=f(3)=
.
∴函数f(x)的值域[2,
].
| 1+x |
| 1-x |
| t-1 |
| t+1 |
∴
| 1+x2 |
| 1-x2 |
1+(
| ||
1-(
|
| t2+1 |
| 2t |
| 1 |
| 2 |
| 1 |
| t |
f(t)=2×
| 1 |
| 2 |
| 1 |
| t |
| 1 |
| t |
即f(x)=x+
| 1 |
| x |
(2)∵f′(x)=1-
| 1 |
| x2 |
| x2-1 |
| x2 |
在区间[
| 1 |
| 2 |
f(x)min=f(1)=2,
而f(
| 1 |
| 2 |
| 5 |
| 2 |
| 10 |
| 3 |
| 10 |
| 3 |
∴函数f(x)的值域[2,
| 10 |
| 3 |

练习册系列答案
相关题目
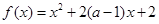 在区间
在区间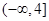 内递减,那么实数
内递减,那么实数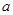 的取值范围为( )
的取值范围为( )