题目内容
已知双曲线 与抛物线
与抛物线 有一个公共的焦点
有一个公共的焦点 ,且两曲线的一个交点为
,且两曲线的一个交点为 ,若
,若 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A. | B. | C.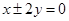 | D. |
B
解析试题分析:抛物线 得出其焦点坐标(2,0),故双曲线中c=2,
得出其焦点坐标(2,0),故双曲线中c=2,
又|PF|=5,设P(m,n),则|PF|=m+2
∴m+2=5,m=3,
∴点P的坐标(3,±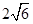 ),
),
∴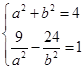
解得,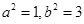 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为
故选B。
考点:本题主要考查抛物线的几何性质,双曲线的几何性质。
点评:小综合题,将几种曲线柔和在一起进行考查,是高考命题的一个特点,本题主要考查a,b,c,e,p的关系,也是高考考查的重点。

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
抛物线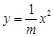 的焦点坐标为( )
的焦点坐标为( )
A.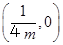 | B.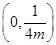 | C.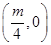 | D.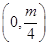 |
椭圆 的两焦点之间的距离为
的两焦点之间的距离为
A. | B. | C. | D. |
抛物线 的焦点F是椭圆
的焦点F是椭圆 的一个焦点,且它们的交点M到F的距离为
的一个焦点,且它们的交点M到F的距离为 ,则椭圆的离心率为
,则椭圆的离心率为
A. | B. | C. | D. |
抛物线 的焦点到双曲线
的焦点到双曲线 的渐近线的距离为( )
的渐近线的距离为( )
A. | B. | C. | D. |
已知函数 是偶函数,则函数的图象与y轴交点的纵坐标的最大值为:( )
是偶函数,则函数的图象与y轴交点的纵坐标的最大值为:( )
| A.-4 | B.2 | C.3 | D.4 |
 和
和 为双曲线
为双曲线 (
( )的两个焦点, 若点
)的两个焦点, 若点 和点
和点 是正三角形的三个顶点,则双曲线的离心率为( )。
是正三角形的三个顶点,则双曲线的离心率为( )。


 的左右焦点分别为
的左右焦点分别为 ,若椭圆
,若椭圆 上恰好有6个不同的点
上恰好有6个不同的点 ,使得
,使得 为等腰三角形,则椭圆
为等腰三角形,则椭圆



 ,它的一个焦点为F1,则满足
,它的一个焦点为F1,则满足 为等边三角形的椭圆的离心率是( )
为等边三角形的椭圆的离心率是( )


