题目内容
【题目】已知椭圆![]() :
:![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,上、下顶点为
,上、下顶点为![]() ,
,![]() ,四边形
,四边形![]() 是面积为2的正方形.
是面积为2的正方形.
(1)求椭圆的标准方程;
(2)已知点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)利用正方形的面积和边长关系列方程组,结合![]() 解方程组求得
解方程组求得![]() 的值,进而求得椭圆的标准方程.
的值,进而求得椭圆的标准方程.
(2)当直线![]() 斜率不存在时,根据对称性判断出
斜率不存在时,根据对称性判断出![]() ;当直线
;当直线![]() 斜率存在时,设出直线
斜率存在时,设出直线![]() 的方程,联立直线的方程和椭圆方程,化简后写出韦达定理,计算
的方程,联立直线的方程和椭圆方程,化简后写出韦达定理,计算![]() ,由此证得
,由此证得![]() .
.
(1)解:∵四边形![]() 是面积为2的正方形,
是面积为2的正方形,
∴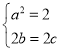 ,
,
又![]() ,∴
,∴![]() ,
,
则椭圆![]() 的标准方程是
的标准方程是![]() ;
;
(2)证明:由(1)知,![]() ,
,
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 轴,
轴,
则点![]() ,
,![]() 关于
关于![]() 轴对称,
轴对称,
此时有,![]() ;
;
当直线![]() 的斜率存在时,
的斜率存在时,
设直线![]() 的方程为
的方程为![]() ,
,
联立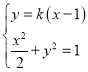 消去
消去![]() 得,
得,
![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]()
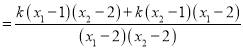
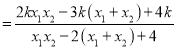
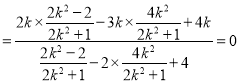 ,
,
即![]() ,∴
,∴![]() .
.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案【题目】千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区![]() 的
的![]() 天日落和夜晚天气,得到如下
天日落和夜晚天气,得到如下![]() 列联表:
列联表:
夜晚天气日落云里走 | 下雨 | 未下雨 |
出现 |
|
|
未出现 |
|
|
参考公式: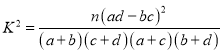 .
.
临界值表:
|
|
|
|
|
|
|
|
|
|
(1)根据上面的列联表判断能否有![]() 的把握认为“当晚下雨”与“‘日落云里走’出现”有关?
的把握认为“当晚下雨”与“‘日落云里走’出现”有关?
(2)小波同学为进一步认识其规律,对相关数据进行分析,现从上述调查的“夜晚未下雨”天气中按分层抽样法抽取![]() 天,再从这
天,再从这![]() 天中随机抽出
天中随机抽出![]() 天进行数据分析,求抽到的这
天进行数据分析,求抽到的这![]() 天中仅有
天中仅有![]() 天出现“日落云里走”的概率.
天出现“日落云里走”的概率.
【题目】第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行,赛期10天,共设置射击、游泳、田径、篮球等27个大项,329个小项,共有来自100多个国家的近万名现役军人同台竞技.前期为迎接军运会顺利召开,特招聘了3万名志愿者.某部门为了了解志愿者的基本情况,调查了其中100名志愿者的年龄,得到了他们年龄的中位数为34岁,年龄在![]() 岁内的人数为15人,并根据调查结果画出如所示的频率分布直方图:
岁内的人数为15人,并根据调查结果画出如所示的频率分布直方图:
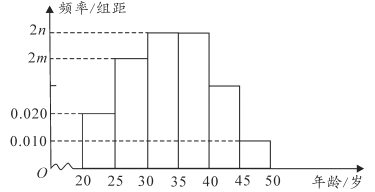
(1)求![]() ,
,![]() 的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
(2)本次军运会志愿者主要通过直接到武汉军运会执委会志愿者部现场报名和登录第七届世界军运会官网报名,即现场和网络两种方式报名调查.这100位志愿者的报名方式部分数据如下表所示,完善下面的表格,通过计算说明能否在犯错误的概率不超过0.001的前提下,认为“选择哪种报名方式与性别有关系”?
男性 | 女性 | 总计 | |
现场报名 | 50 | ||
网络报名 | 31 | ||
总计 | 50 |
参考公式及数据: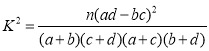 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
3.841 | 6.635 | 7.879 | 10.828 |