题目内容
【题目】如图,某校打算在长为1千米的主干道![]() 一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域
一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域![]() (
(![]() 为直角)和以
为直角)和以![]() 为直径的半圆形区域组成,点
为直径的半圆形区域组成,点![]() (异于
(异于![]() ,
,![]() )为半圆弧上一点,点
)为半圆弧上一点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,设
,设![]() ,且
,且![]() .初步设想把咨询台安排在线段
.初步设想把咨询台安排在线段![]() ,
,![]() 上,把宣传海报悬挂在弧
上,把宣传海报悬挂在弧![]() 和线段
和线段![]() 上.
上.
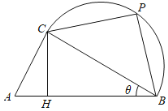
(1)若为了让学生获得更多的咨询机会,让更多的省内高校参展,打算让![]() 最大,求该最大值;
最大,求该最大值;
(2)若为了让学生了解更多的省外高校,贴出更多高校的海报,打算让弧![]() 和线段
和线段![]() 的长度之和最大,求此时的
的长度之和最大,求此时的![]() 的值.
的值.
【答案】(1)![]() ; (2)
; (2)![]()
【解析】
(1)由题意,结合三角恒等变换的公式,求得![]() ,再利用三角函数的性质,即可求解;
,再利用三角函数的性质,即可求解;
(2)由题意,取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,求得弧长
,求得弧长![]() 和线段
和线段![]() 的长度之和表达式
的长度之和表达式![]() ,设
,设![]() ,
,![]() ,得到
,得到![]() ,结合导数求得函数的单调性和最值,即可求解.
,结合导数求得函数的单调性和最值,即可求解.
(1)由题意,在![]() 中,可得
中,可得![]() ,
,
在![]() 中,可得
中,可得![]() ,
,
在![]() 中,可得
中,可得![]() ,
,
所以![]()
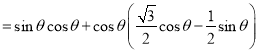
![]()
![]()
![]() .
.
因为![]() ,则
,则![]() ,
,
所以当且仅当![]() ,即
,即![]() 时,
时,![]() 取得最大值,且最大值为
取得最大值,且最大值为![]() 千米.
千米.
(2)取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() .
.
由(1)知,![]() ,
,![]()
故![]() 的长为
的长为![]() ,
,
则![]() 和线段
和线段![]() 的长度之和
的长度之和
![]()
![]() ,
,![]() .
.
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
故函数![]() 在区间
在区间![]() 上单调递减,故
上单调递减,故![]() .
.
易知函数![]() 在区间
在区间![]() 上也单调递减,所以
上也单调递减,所以![]() ,
,
所以![]() ,
,
所以当且仅当![]() 时,
时,![]() 和线段
和线段![]() 的长度之和最大.
的长度之和最大.

练习册系列答案
相关题目