题目内容
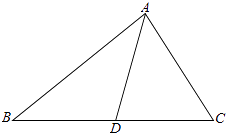
【题目】如图1,在直角梯形![]() 中,AB∥CD,
中,AB∥CD,![]() ,且
,且![]() .现以
.现以![]() 为一边向梯形外作正方形
为一边向梯形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
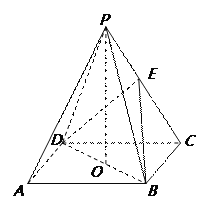
将正方形![]() 翻折,使平面
翻折,使平面![]() 与平面
与平面![]() 垂直,如图2.
垂直,如图2.


(Ⅰ)求证:BC⊥平面DBE;
(Ⅱ)求点D到平面BEC的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)要证直线![]() 与平面
与平面![]() 垂直,题中翻折成平面
垂直,题中翻折成平面![]() 与平面
与平面![]() 垂直,因此有
垂直,因此有![]() 平面
平面![]() ,从而有一个线线垂直
,从而有一个线线垂直![]() ,另一个在梯形
,另一个在梯形![]() 中由平面几何知识可证
中由平面几何知识可证![]() ,从而得证线面垂直;(2)由(1)知平面
,从而得证线面垂直;(2)由(1)知平面![]() 与平面
与平面![]() 垂直,因此只要过
垂直,因此只要过![]() 作
作![]() 于点
于点![]() ,则可得
,则可得![]() 的长就是点
的长就是点![]() 到平面
到平面![]() 的距离,在三角形中计算可得.
的距离,在三角形中计算可得.
试题解析:(1)在正方形![]() 中,
中,![]() ,又因为平面
,又因为平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .在直角梯形
.在直角梯形![]() 中,
中,![]() ,可得
,可得![]() ,在
,在![]() 中,
中,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() 平面
平面![]() .
.
(2)因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离等于线段
的距离等于线段![]() 的长度.
的长度.
在直角三角形![]() 中,
中,![]() ,所以
,所以![]() ,
,
所以点![]() 到平面
到平面![]() 的距离等于
的距离等于![]() .
.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目