题目内容
【题目】设A、B为抛物线C:![]() 上两点,A与B的中点的横坐标为2,直线AB的斜率为1.
上两点,A与B的中点的横坐标为2,直线AB的斜率为1.
(Ⅰ)求抛物线C的方程;
(Ⅱ)直线![]() 交x轴于点M,交抛物线C:
交x轴于点M,交抛物线C:![]() 于点P,M关于点P的对称点为N,连结ON并延长交C于点H.除H以外,直线MH与C是否有其他公共点?请说明理由.
于点P,M关于点P的对称点为N,连结ON并延长交C于点H.除H以外,直线MH与C是否有其他公共点?请说明理由.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.
【解析】
(Ⅰ)设 ![]() ,直线
,直线![]() 的斜率为
的斜率为![]() 1,又因为
1,又因为![]() 都在曲线
都在曲线![]() 上,
上,![]() ,
, ![]() ,结合
,结合![]() 利用点差法可得p = 2,从而可得结果;(Ⅱ)求得点
利用点差法可得p = 2,从而可得结果;(Ⅱ)求得点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() , 从而可得直线
, 从而可得直线![]() 的方程为
的方程为![]() ,联立方程
,联立方程
解得点![]() 的坐标为
的坐标为![]() ,可得直线
,可得直线![]() 的方程为
的方程为![]() ,联立方程,整理得
,联立方程,整理得![]() ,利用
,利用![]() ,可得结论.
,可得结论.
(Ⅰ)设 ![]() ,AB 直线的斜率为1,又因为A,B都在曲线C上,
,AB 直线的斜率为1,又因为A,B都在曲线C上,
所以![]() ①
① ![]() ②
②
-得![]() ,
,
![]() 得
得![]() ,得p = 2,所以抛物线C的方程是
,得p = 2,所以抛物线C的方程是![]() .
.
(Ⅱ)由题意,可知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,
,
从而可得直线![]() 的方程为
的方程为![]() ,联立方程
,联立方程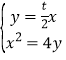 ,
,
解得![]() .
.
依题意,点![]() 的坐标为
的坐标为![]() ,由于
,由于![]() ,
,![]() ,可得直线
,可得直线![]() 的方程为
的方程为![]() ,
,
联立方程![]() ,整理得
,整理得![]() ,
,
则![]() ,从而可知
,从而可知![]() 和
和![]() 只有一个公共点
只有一个公共点![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目

