题目内容
【题目】椭圆的两个焦点坐标分别为F1(-![]() ,0)和F2(
,0)和F2(![]() ,0),且椭圆过点
,0),且椭圆过点![]()
(1)求椭圆方程;
(2)过点![]() 作不与y轴垂直的直线l交该椭圆于M,N两点,A为椭圆的左顶点,证明
作不与y轴垂直的直线l交该椭圆于M,N两点,A为椭圆的左顶点,证明![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)设椭圆方程为![]() ,由题设代入点的坐标,求得
,由题设代入点的坐标,求得![]() ,即可得到椭圆的方程;
,即可得到椭圆的方程;
(2)设直线的方程![]() ,联立方程组,利用根与系数的关系,得到
,联立方程组,利用根与系数的关系,得到![]() ,再由向量的数量积的运算求得
,再由向量的数量积的运算求得![]() ,即可得到答案.
,即可得到答案.
解:(1)设椭圆方程为![]() ,
,
由![]() ,椭圆过点
,椭圆过点![]() 可得
可得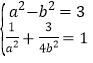 ,
,
解得![]() 所以可得椭圆方程为
所以可得椭圆方程为![]() .
.
(2)由题意可设直线MN的方程为:![]() ,
,
联立直线MN和椭圆的方程: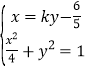
化简得(k2+4)y2-![]() ky-
ky-![]() =0.
=0.
设M(x1,y1),N(x2,y2),
则y1y2=![]() ,y1+y2=
,y1+y2=![]()
又A(-2,0),则![]() =(x1+2,y1)·(x2+2,y2)=(k2+1)y1y2+
=(x1+2,y1)·(x2+2,y2)=(k2+1)y1y2+![]() k(y1+y2)+
k(y1+y2)+![]() =0,
=0,
所以![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


