题目内容
【题目】对于任意实数a,b,定义max{a,b}=![]() , 已知在[﹣2,2]上的偶函数f(x)满足当0≤x≤2时,f(x)=max{2x﹣1,2﹣x}若方程f(x)﹣mx+1=0恰有两个根,则m的取值范围是( )
, 已知在[﹣2,2]上的偶函数f(x)满足当0≤x≤2时,f(x)=max{2x﹣1,2﹣x}若方程f(x)﹣mx+1=0恰有两个根,则m的取值范围是( )
A.[﹣2,﹣eln2)∪(eln2,2]
B.[﹣eln2,0)∪(0,eln2]
C.[﹣2,0)∪(0,2]
D.[﹣e,﹣2)∪(2,e]
【答案】A
【解析】当1≤x≤2时,2x﹣1>2﹣x,此时f(x)=2x﹣1,
当0≤x≤1时,2x﹣1<2﹣x,此时f(x)=2﹣x,
即f(x)=![]() ,
,
若﹣2≤x≤﹣1,则1≤﹣x≤2,此时f(﹣x)=2﹣x﹣1,
∵f(x)是偶函数,
∴f(x)=f(﹣x)=2﹣x﹣1,﹣2≤x≤﹣1.
若﹣1≤x≤0,则0≤﹣x≤1,此时f(﹣x)=2﹣x,
∵f(x)是偶函数,
∴f(x)=f(﹣x)=2﹣x,﹣1≤x≤0.
作出函数f(x)的图象如图:
由f(x)﹣mx+1=0得f(x)=mx﹣1,
设g(x)=mx﹣1,
则当m=0时,f(x)与g(x)没有交点,此时不满足条件.
当m>0时,当x=1,f(1)=1,当x=2时,f(2)=3,
当直线经过A(1,1)时,此时m﹣1=1,则m=2,此时g(x)=2x﹣1,
g(2)=3,即直线g(x)=2x﹣1经过A,C点,此时两个曲线有两个交点,满足条件,
当直线y=mx﹣1与f(x)=2x﹣1相切时,
设切点为(k,n),
则f′(k)=2kln2,且2k﹣1=n,
则切线方程为y﹣n=2kln2(x﹣k),
即y=(2kln2)x﹣k2kln2+2k﹣1,
即2kln2=m,且﹣k2kln2+2k﹣1=﹣1,
即2kln2=m,且﹣k2kln2+2k=0,
2kln2=m,且﹣kln2+1=0,
即kln2=1,解得k=![]() =log2e,
=log2e,
则m=![]() =eln2,
=eln2,
此时直线和f(x)只有一个交点,
若时两个曲线有两个交点,则eln2<m≤2,
根据偶函数的对称性知当m<0时,﹣2≤m<eln2,
综上m的取值范围是[﹣2,﹣eln2)∪(eln2,2],
故选:A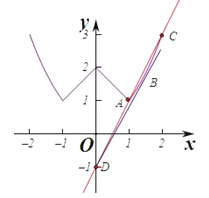
根据条件先求出当0≤x≤2时,函数f(x)的解析式,然后根据偶函数的性质求出函数在[﹣2,2]上解析式,利用函数与方程之间的关系转化为两个函数的相交问题,结合导数的几何意义求出切线斜率进行求解即可。

【题目】某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据如表所示
参加社团活动 | 不参加社团活动 | 合计 | |
学习积极性高 | 17 | 8 | 25 |
学习积极性一般 | 5 | 20 | 25 |
合计 | 22 | 28 | 50 |
(Ⅰ)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(Ⅱ)试运用独立性检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
x2=![]() .
.
P(x2≥k) | 0.05 | 0.01 | 0.001 |
K | 3.841 | 6.635 | 10.828 |

