题目内容
【题目】如图,点F1(﹣c,0),F2(c,0)分别是椭圆C: ![]() (a>b>0)的左右焦点,经过F1做x轴的垂线交椭圆C的上半部分于点P,过点F2作直线PF2垂线交直线
(a>b>0)的左右焦点,经过F1做x轴的垂线交椭圆C的上半部分于点P,过点F2作直线PF2垂线交直线 ![]() 于点Q.
于点Q.
(Ⅰ)如果点Q的坐标是(4,4),求此时椭圆C的方程;
(Ⅱ)证明:直线PQ与椭圆C只有一个交点.
【答案】解:(Ⅰ)将点P(﹣c,y1)(y1>0)代入 ![]() 得
得 ![]()
∴P 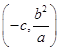
∵点Q的坐标是(4,4),PF2⊥QF2
∴ 
∵ ![]()
∴a=2,c=1,b= ![]()
∴椭圆C的方程为 ![]() ;
;
(Ⅱ)证明:设Q 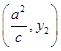 ,∵PF2⊥QF2
,∵PF2⊥QF2
∴ 
∴y2=2a
∴ 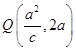
∵P 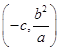 ,∴
,∴ 
∵ ![]() ,∴
,∴ ![]()
∴y′= 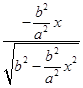
∴当x=﹣c时,y′= 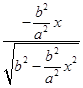 =
= ![]()
∴直线PQ与椭圆C只有一个交点
【解析】(Ⅰ)将点P(﹣c,y1)(y1>0)代入 ![]() ,可求得P
,可求得P ![]() ,根据点Q的坐标是(4,4),PF1⊥QF2 , 即可求得椭圆C的方程;(Ⅱ)利用PF1⊥QF2 , 求得
,根据点Q的坐标是(4,4),PF1⊥QF2 , 即可求得椭圆C的方程;(Ⅱ)利用PF1⊥QF2 , 求得 ![]() ,从而可求
,从而可求 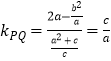 ,又
,又 ![]() ,求导函数,可得x=﹣c时,y′=
,求导函数,可得x=﹣c时,y′=  =
= ![]() ,故可知直线PQ与椭圆C只有一个交点.
,故可知直线PQ与椭圆C只有一个交点.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
