题目内容
17．设?x∈（1，2），使|x-a|≤6-2x成立．则正数a的取值范围是？分析 作出函数y=|x-a|（a＞0）的图象与直线y=6-2x，数形结合求得答案．
解答 解：作出函数y=|x-a|（a＞0）与直线y=6-2x的图象如图，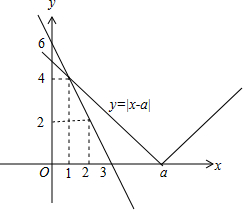
把（1，4）代入数y=|x-a|（a＞0），得4=|1-a|，解得a=5．
∴当0＜a≤5时，?x∈（1，2），使|x-a|≤6-2x成立．
点评 本题借助考查特称命题，考查数形结合解决问题的能力，属中档题．
练习册系列答案
阅读快车系列答案
相关题目
7．圆的方程是（x-cosθ）2+（y-sinθ）2=$\frac{1}{2}$，当θ从0变化到2π时，动圆所扫过的面积是（ ）
| A． | π | B． | 2$\sqrt{2}$π | C． | （1+$\sqrt{2}$）π | D． | （1+$\frac{\sqrt{2}}{2}$）2π |
8．若α，β∈（0，$\frac{π}{2}$）且tanα=$\frac{1}{2}$，tanβ=$\frac{1}{3}$，则tan（α+β）等于（ ）
| A． | -1 | B． | 1 | C． | $\frac{3}{2}$ | D． | -$\frac{3}{2}$ |
12．若N＞1，logaN＞logbN．且a+b=1，则有（ ）
| A． | 1＜a＜b | B． | 0＜a＜b＜1 | C． | 1＜b＜a | D． | 0＜b＜a＜1 |
6．已知集合A={x丨y=lg（x-x2）}，B={x丨x2-cx＜0，c＞0}，若A⊆B，则实数c的取值范围是（ ）
| A． | （0，1] | B． | [1，+∞） | C． | （0，1） | D． | （1，+∞） |