Question

【题目】在斜三棱柱A1B1C1-ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC．

（1）若D是BC的中点，求证：AD⊥CC1；

（2）过侧面BB1C1C的对角线BC1的平面交侧棱于M，若AM=MA1，求证：截面MBC1⊥侧面BB1C1C．

Answer 1

【答案】(1)详见解析 (2)详见解析

【解析】

（1）由AB=AC，且D是BC的中点得到AD⊥BC，再由侧面BB1C1C⊥底面ABC，结合面面垂直的性质得到AD⊥侧面BB1C1C．从而证得答案； （2）由AM=MA1，可想到延长B1A1与BM交于N，连结C1N，由中位线知识结合已知得到A1C1=A1N=A1B1，∴C1N⊥C1B1，然后由面面垂直的性质及判定得答案．

（1）如图，

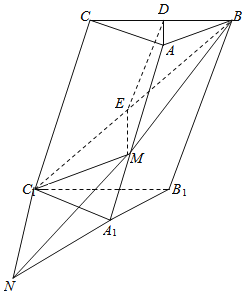
∵AB=AC，D是BC的中点，∴AD⊥BC，

∵底面ABC⊥平面BB1C1C，

由两面垂直的性质，∴AD⊥侧面BB1C1C．

又CC1面BB1C1C，∴AD⊥CC1；

（2）延长B1A1与BM的延长线交于N，连结C1N，

∵AM=MA1，且MA1∥BB1，∴NA1=A1B1，

∵AB=AC，∴A1B1=A1C1，∴A1C1=A1N=A1B1，

∴A1为△B1C1N外接圆的圆心，

∴C1N⊥C1B1，

∵底面NB1C1⊥侧面BB1C1C，

由面面垂直的性质，∴C1N⊥侧面BB1C1C，

∴截面C1NB⊥侧面BB1C1C，∴截面MBC1⊥侧面BB1C1C．