题目内容
已知函数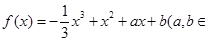
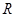 ).
).
(Ⅰ) 若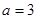 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(Ⅱ) 若函数 在其图象上任意一点
在其图象上任意一点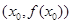 处切线的斜率都小于
处切线的斜率都小于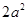 ,求实数
,求实数 的取值范围.
的取值范围.
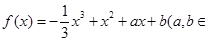
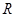 ).
).(Ⅰ) 若
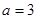 ,试确定函数
,试确定函数 的单调区间;
的单调区间;(Ⅱ) 若函数
 在其图象上任意一点
在其图象上任意一点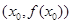 处切线的斜率都小于
处切线的斜率都小于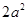 ,求实数
,求实数 的取值范围.
的取值范围.(Ⅰ)单调增区间为
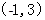 ,减区间为
,减区间为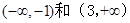
(Ⅱ)
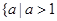 或
或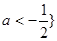
本试题主要是考查了导数在研究函数中的运用。利用导数符号与函数单调性的关系得到求解,同时考查了导数的几何意义的运用。
(1)由于函数的导函数为二次函数,借助于二次不等式得到增减区间。
(2)利用导数要使得函数 在其图象上任意一点
在其图象上任意一点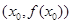 处切线的斜率都小于
处切线的斜率都小于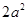 ,则只要导数恒小于
,则只要导数恒小于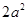 即可,转化为恒成立问题来解得。
即可,转化为恒成立问题来解得。

因为对任意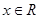 ,
,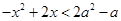 恒成立, 所以
恒成立, 所以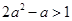 ,解得
,解得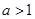 或
或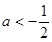 , 所以,实数
, 所以,实数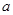 的取值范围为
的取值范围为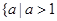 或
或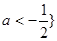 .
.
(1)由于函数的导函数为二次函数,借助于二次不等式得到增减区间。
(2)利用导数要使得函数
 在其图象上任意一点
在其图象上任意一点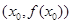 处切线的斜率都小于
处切线的斜率都小于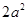 ,则只要导数恒小于
,则只要导数恒小于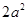 即可,转化为恒成立问题来解得。
即可,转化为恒成立问题来解得。
因为对任意
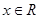 ,
,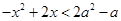 恒成立, 所以
恒成立, 所以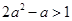 ,解得
,解得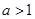 或
或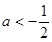 , 所以,实数
, 所以,实数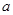 的取值范围为
的取值范围为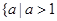 或
或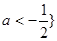 .
. 
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
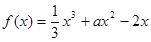 在区间
在区间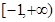 上有极大值和极小值,则实数
上有极大值和极小值,则实数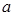 的取值范围是
的取值范围是 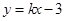 与曲线
与曲线 相切,则实数
相切,则实数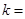 .
.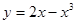 在x=-1处的切线方程为( )
在x=-1处的切线方程为( )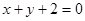
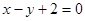
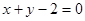
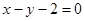
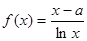 ,其中
,其中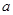 为实数.
为实数.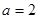 时,求曲线
时,求曲线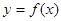 在点
在点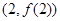 处的切线方程;
处的切线方程;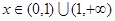 ,
,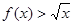 恒成立?若不存在,请说明理由,若存在,求出
恒成立?若不存在,请说明理由,若存在,求出 在
在 处的切线方程为 .
处的切线方程为 . 在区间
在区间 上不单调,则实数
上不单调,则实数 的范围是 .
的范围是 .