题目内容
若直线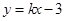 与曲线
与曲线 相切,则实数
相切,则实数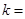 .
.
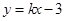 与曲线
与曲线 相切,则实数
相切,则实数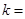 .
.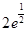
解:∵y=2lnx,
∴y'=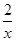 ,设切点为(m,2lnm),得切线的斜率为2 m,
,设切点为(m,2lnm),得切线的斜率为2 m,
所以曲线在点(m,2lnm)处的切线方程为:
y-2lnm="2" m ×(x-m).
它过点(0,-3),∴-3-2lnm=-2,
∴m="e" -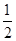 ,
,
∴k="2" m ="2" e故答案为:2 e .
∴y'=
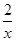 ,设切点为(m,2lnm),得切线的斜率为2 m,
,设切点为(m,2lnm),得切线的斜率为2 m,所以曲线在点(m,2lnm)处的切线方程为:
y-2lnm="2" m ×(x-m).
它过点(0,-3),∴-3-2lnm=-2,
∴m="e" -
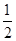 ,
,∴k="2" m ="2" e故答案为:2 e .

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
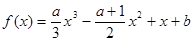 ,其中
,其中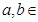 R.
R.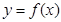 在点
在点 处的切线方程为
处的切线方程为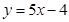 ,求函数
,求函数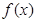 的解析
的解析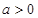 时,讨论函数
时,讨论函数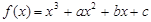 ,曲线
,曲线 上点
上点 处的切线方程为
处的切线方程为
 在
在 时有极值,求函数
时有极值,求函数 上的最大值;
上的最大值; 上单调递增,求
上单调递增,求 的取值范围.
的取值范围. 上切线倾斜角为
上切线倾斜角为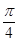 的点是( )
的点是( )

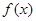 的定义域为
的定义域为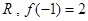 ,对任意
,对任意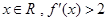 ,则
,则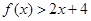 的解集为( )
的解集为( )
 上一点P处的切线与直线
上一点P处的切线与直线 平行,则点P的坐标为_______
平行,则点P的坐标为_______ 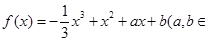
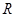 ).
).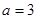 ,试确定函数
,试确定函数 的单调区间;
的单调区间;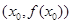 处切线的斜率都小于
处切线的斜率都小于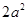 ,求实数
,求实数 的取值范围.
的取值范围.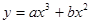 ,当
,当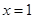 时,有极大值
时,有极大值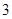 。
。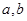 的值;
的值;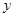 的极小值。
的极小值。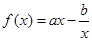 ,曲线
,曲线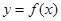 在点
在点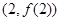 处的切线方程为
处的切线方程为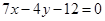 .
.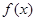 的解析式;(2)证明:曲线
的解析式;(2)证明:曲线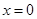 和直线
和直线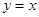 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.