题目内容
4．在△ABC中，若a=1，c=$\frac{\sqrt{2}}{2}$，∠C=40°，则符合题意的b的值有2个．分析 利用余弦定理列出关系式，将a，c及cosC的值代入，得到关于b的一元二次方程，表示出根的判别式，判断其值大于0，得到方程有两个不相等的实数根，即可确定出b的个数．
解答 解：∵a=1，c=$\frac{\sqrt{2}}{2}$，cosC=cos40°，
∴由余弦定理得：c2=a2+b2-2ab•cosC，即$\frac{1}{2}$=1+b2-2b•cos40°，
整理得：2b2-4cos40°b+1=0，
∵△=（4cos40°）2-8＞0，
∴方程有2实数根，
则符合题意b的值有2个．
故答案为：2．
点评 此题考查了余弦定理，以及根的判别式与方程解的关系，熟练掌握余弦定理是解本题的关键，属于中档题．
练习册系列答案
相关题目
14．直线2x-y+1=0关于y轴对称的直线方程是（ ）
| A． | 2x+y-1=0 | B． | 2x+y+1=0 | C． | 2x-y+1=0 | D． | 2x-y-1=0 |
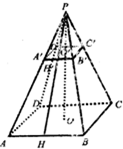如图所示，正四棱锥P-ABCD被过棱锥高上O′点且平行底面的平面A′B′C′D′所截，得到正四棱台OO′和较小的棱锥PO′，其中O′分PO为$\frac{PO′}{OO′}$=$\frac{1}{2}$，侧棱PA长为15cm，小棱锥底面边长A′B′为6cm．
将正偶数列{2n}中的所有项按每一行比上一行多一项的规则排成如图数表：记aij是这个数表的第i行第j列的数．例如a43=18．