题目内容
如图椭圆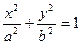 (a>b>0)的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上.
(a>b>0)的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上.
(1)求椭圆的离心率;
(2)若平行四边形OCED的面积为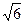 , 求椭圆方程.
, 求椭圆方程.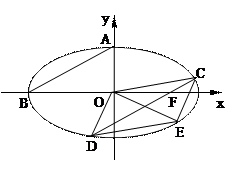
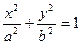 (a>b>0)的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上.
(a>b>0)的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上.(1)求椭圆的离心率;
(2)若平行四边形OCED的面积为
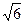 , 求椭圆方程.
, 求椭圆方程.
)(1)e =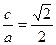 . (2)故椭圆方程为
. (2)故椭圆方程为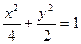
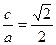 . (2)故椭圆方程为
. (2)故椭圆方程为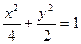
(1) ∵焦点为F(c, 0), AB斜率为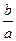 , 故CD方程为y=
, 故CD方程为y=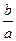 (x-c). 于椭圆联立后消去y得2x2-2cx-b2="0." ∵CD的中点为G(
(x-c). 于椭圆联立后消去y得2x2-2cx-b2="0." ∵CD的中点为G(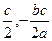 ), 点E(c, -
), 点E(c, -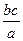 )在椭圆上, ∴将E(c, -
)在椭圆上, ∴将E(c, -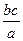 )代入椭圆方程并整理得2c2=a2, ∴e =
)代入椭圆方程并整理得2c2=a2, ∴e =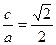 .
.
(2)由(Ⅰ)知CD的方程为y=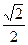 (x-c), b="c," a=
(x-c), b="c," a=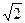 c.
c.
与椭圆联立消去y得2x2-2cx-c2=0.
∵平行四边形OCED的面积为
S=c|yC-yD|=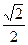 c
c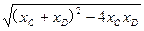 =
=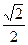 c
c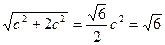 ,
,
∴c=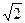 , a="2," b=
, a="2," b=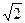 . 故椭圆方程为
. 故椭圆方程为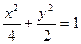
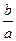 , 故CD方程为y=
, 故CD方程为y=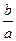 (x-c). 于椭圆联立后消去y得2x2-2cx-b2="0." ∵CD的中点为G(
(x-c). 于椭圆联立后消去y得2x2-2cx-b2="0." ∵CD的中点为G(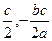 ), 点E(c, -
), 点E(c, -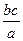 )在椭圆上, ∴将E(c, -
)在椭圆上, ∴将E(c, -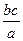 )代入椭圆方程并整理得2c2=a2, ∴e =
)代入椭圆方程并整理得2c2=a2, ∴e =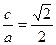 .
. (2)由(Ⅰ)知CD的方程为y=
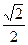 (x-c), b="c," a=
(x-c), b="c," a=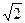 c.
c. 与椭圆联立消去y得2x2-2cx-c2=0.
∵平行四边形OCED的面积为
S=c|yC-yD|=
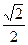 c
c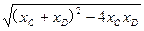 =
=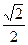 c
c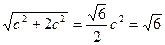 ,
, ∴c=
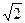 , a="2," b=
, a="2," b=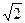 . 故椭圆方程为
. 故椭圆方程为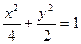

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
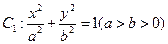 的左、右焦点分别为
的左、右焦点分别为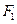 、
、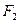 ,其中
,其中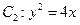 的焦点,
的焦点,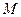 是
是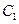 与
与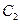 在第一象限的交点,且
在第一象限的交点,且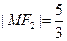 .
.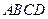 的顶点
的顶点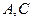 在椭圆
在椭圆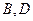 在直线
在直线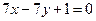 上,求直线
上,求直线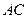 的方程.
的方程.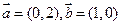 ,过定点
,过定点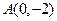 ,以
,以 方向向量的直线与经过点
方向向量的直线与经过点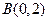 ,以向量
,以向量 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中
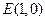 的直线
的直线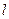 与C交于两个不同点M、N,求
与C交于两个不同点M、N,求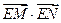 的取值范围
的取值范围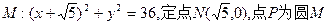 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足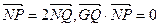 .
. ,与曲线C交于A、B两点,O是坐标原点,设
,与曲线C交于A、B两点,O是坐标原点,设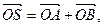 是否存在这样的直线
是否存在这样的直线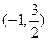 ;
;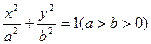 的左右焦点分别为
的左右焦点分别为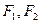 ,
,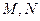 是椭圆右准线上的两个动点,且
是椭圆右准线上的两个动点,且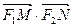 =0.
=0.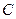 是以
是以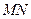 为直径的圆,试判断原点
为直径的圆,试判断原点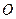 与圆
与圆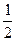 ,
,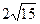 ,求椭圆的方程
,求椭圆的方程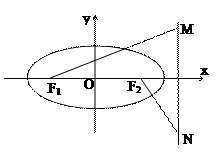
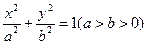 的离心率
的离心率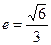 ,
,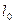 为过点
为过点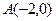 和上顶点
和上顶点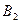 的直线,下顶点
的直线,下顶点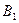 与
与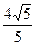 .
.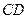 交
交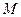 , 若
, 若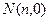 ,试求
,试求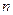 的范围.
的范围.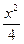 +y2=1相交于A、B两点,则|AB|的最大值是( )
+y2=1相交于A、B两点,则|AB|的最大值是( )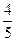
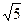 C.
C.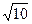 D.
D.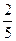
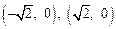 ,则PC·PD的最大值为 .
,则PC·PD的最大值为 .