题目内容
9．
一半径为6米的水轮如图，水轮圆心O距离水面3米，已知水轮每分钟转动4圈，水轮上点P从水中浮现时开始到其第一次达到最高点的用时为5秒．
分析 由已知可得水轮上点P从水中浮现时开始到其第一次达到最高点要旋转120°，即$\frac{1}{3}$个周期，进而根据水轮每分钟转动4圈，求出周期，可得答案．
解答 解：过O作水平的垂线，垂足为Q，如下图所示：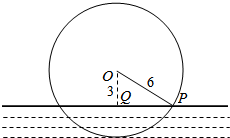
由已知可得：OQ=3，OP=6，
则cos∠POQ=$\frac{1}{2}$，即∠POQ=60°，
则水轮上点P从水中浮现时开始到其第一次达到最高点要旋转120°，即$\frac{1}{3}$个周期，
又由水轮每分钟转动4圈，可知周期是15秒，
故水轮上点P从水中浮现时开始到其第一次达到最高点的用时为5秒，
故答案为：5
点评 本题考查的知识点是三角函数的周期，在实际问题中建立三角函数模型的问题．难度不大，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．在用反证法证明命题“已知a，b，c∈（0，2），求证a（2-b），b（2-c），c（2-a）不可能都大于1”时，反证假设时正确的是（ ）
| A． | 假设a（2-b），b（2-c），c（2-a）都小于1 | B． | 假设a（2-b），b（2-c），c（2-a）都大于1 | ||
| C． | 假设a（2-b），b（2-c），c（2-a）都不大于1 | D． | 以上都不对 |
20．设直角三角形中两锐角为A和B，则cosAcosB的取值范围是（ ）
| A． | （0，$\frac{1}{2}$] | B． | （0，1） | C． | [$\frac{1}{2}$，1） | D． | [$\frac{\sqrt{3}}{4}$，1） |
