题目内容
20．在复平面上复数-3-2i、-4+5i、2+i所对应的点分别是A，B，C，则平行四边形ABCD的对角线BD所对应的复数是（ ）| A． | 5-9i | B． | -5-3i | C． | 7-11i | D． | -7+11i |
分析 由题意画出图形，根据A，B，C所对应的复数分别为-3-2i、-4+5i、2+i，得到$\overrightarrow{BA}、\overrightarrow{BC}$所对应的复数，然后利用向量加法求得BD所对应的复数．
解答 解：如图，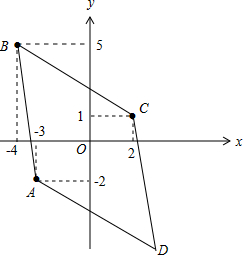
∵A，B，C所对应的复数分别为-3-2i、-4+5i、2+i，
∴$\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}$=（-3-2i）-（-4+5i）=1-7i，
$\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}$=（2+i）-（-4+5i）=6-4i，
$\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{BC}$=（1-7i）+（6-4i）=7-11i．
故选：C．
点评 本题考查复数的代数表示法及其几何意义，考查了复数的加减法运算，是基础的计算题．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
15．复数1+$\sqrt{3}$i的三角形式是（ ）
| A． | cos$\frac{π}{3}$+isin$\frac{π}{3}$ | B． | 2（cos$\frac{π}{3}$+isin$\frac{π}{3}$） | C． | cos$\frac{π}{6}$+isin$\frac{π}{6}$ | D． | 2（cos$\frac{π}{6}$+isin$\frac{π}{6}$） |