题目内容
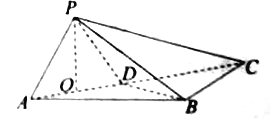
【题目】如图,在三棱锥![]() 中,
中,![]() 为
为![]() 中点,
中点,![]() 在平面
在平面![]() 内的射影
内的射影![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】分析:(1)推导出![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,从而
,从而![]() ,
,![]() ,利用线面垂直的判定定理,即可得到
,利用线面垂直的判定定理,即可得到![]() 面
面![]() ;
;
(2)以![]() 为原点,向量
为原点,向量![]() 的方向分别为
的方向分别为![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() ,求得平面
,求得平面![]() 和平面
和平面![]() 的法向量,利用向量的夹角公式,即可求解.
的法向量,利用向量的夹角公式,即可求解.
详解:(1)因为![]() 在平面
在平面![]() 内的射影
内的射影![]() 在
在![]() 上,所以
上,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
又平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .因为
.因为![]() 平面
平面![]() ,所以
,所以![]() .
.
由已知易得 ![]() ,又
,又![]() ,所以
,所以![]() ,
,
在三角形![]() 中,由余弦定理得,
中,由余弦定理得,![]()
所以![]() ,于是
,于是![]() ,且
,且![]() ·
·
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)在平面![]() 内过
内过![]() 作
作![]() ,则
,则![]() 平面
平面![]() .以
.以![]() 为原点,向量
为原点,向量
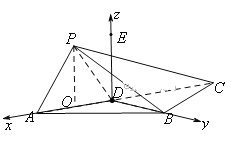
![]() 的方向分别为
的方向分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向,
轴的正方向,
建立空间直角坐标系![]() 为计算简便,不妨设
为计算简便,不妨设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ·
·
所以![]() ,
,![]() .
.
显然![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则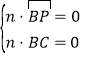 ,即
,即![]() ·
·
令![]() ,得
,得![]() .
.
设二面角![]() 的大小为
的大小为![]() (
(![]() 为锐角).
为锐角).
所以![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某工厂生产某种型号的电视机零配件,为了预测今年![]() 月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度
月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度![]() 月份至
月份至![]() 月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价
月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的
(单位:千件)之间的![]() 组数据如下表所示:
组数据如下表所示:
月份 |
|
|
|
|
|
|
销售单价 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
(1)根据1至![]() 月份的数据,求
月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(2)结合(1)中的线性回归方程,假设该型号电视机零配件的生产成本为每件![]() 元,那么工厂如何制定
元,那么工厂如何制定![]() 月份的销售单价,才能使该月利润达到最大(计算结果精确到
月份的销售单价,才能使该月利润达到最大(计算结果精确到![]() )?
)?
参考公式:回归直线方程![]() ,其中
,其中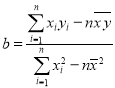 .
.
参考数据:![]() .
.
【题目】某品牌计算机售后保修期为1年,根据大量的维修记录资料,这种品牌的计算机在使用一年内需要维修1次的占15%,需要维修2次的占6%,需要维修3次的占4%.
(1)某人购买了一台这个品牌的计算机,设![]() =“一年内需要维修k次”,k=0,1,2,3,请填写下表:
=“一年内需要维修k次”,k=0,1,2,3,请填写下表:
事件 |
|
|
|
|
概率 |
事件![]() 是否满足两两互斥?是否满足等可能性?
是否满足两两互斥?是否满足等可能性?
(2)求下列事件的概率:
①A=“在1年内需要维修”;
②B=“在1年内不需要维修”;
③C=“在1年内维修不超过1次”.
【题目】某高中尝试进行课堂改革.现高一有![]() 两个成绩相当的班级,其中
两个成绩相当的班级,其中![]() 班级参与改革,
班级参与改革,![]() 班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过
班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过![]() 分的为进步明显,得到如下列联表.
分的为进步明显,得到如下列联表.
进步明显 | 进步不明显 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)是否有![]() 的把握认为成绩进步是否明显与课堂是否改革有关?
的把握认为成绩进步是否明显与课堂是否改革有关?
(2)按照分层抽样的方式从![]() 班中进步明显的学生中抽取
班中进步明显的学生中抽取![]() 人做进一步调查,然后从
人做进一步调查,然后从![]() 人中抽
人中抽![]() 人进行座谈,求这
人进行座谈,求这![]() 人来自不同班级的概率.
人来自不同班级的概率.
附: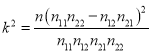 ,当
,当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关.
有关.

