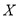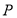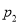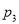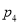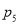题目内容
4. 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.(1)求椭圆C的方程;
(2)若点E的坐标为($\frac{\sqrt{3}}{2}$,0),点A在第一象限且横坐标为$\sqrt{3}$,连结点A与原点O的直线交椭圆C于另一点P,求△PAB的面积;
(3)是否存在点E,使得$\frac{1}{E{A}^{2}}$+$\frac{1}{E{B}^{2}}$为定值?若存在,请指出点E的坐标,并求出该定值;若不存在,请说明理由.
分析 (1)由$\frac{c}{a}=\frac{{\sqrt{6}}}{3}$,设a=3k(k>0),则$c=\sqrt{6}k$,b2=3k2,可设椭圆C的方程为$\frac{x^2}{{9{k^2}}}+\frac{y^2}{{3{k^2}}}=1$,由于直线l垂直于x轴且点E为椭圆C的右焦点,即${x_A}={x_B}=\sqrt{6}k$,代入椭圆方程,解得y即可得出.
(2)将$x=\sqrt{3}$代入$\frac{x^2}{6}+\frac{y^2}{2}=1$,解得y,可得直线AB的方程,与椭圆方程联立解得B,又PA过原点O,可得P,|PA|,直线PA的方程,求出点B到直线PA的距离h,k可得S△PAB=$\frac{1}{2}h|PA|$.
(3)假设存在点E,使得$\frac{1}{{E{A^2}}}+\frac{1}{{E{B^2}}}$为定值,设E(x0,0),当直线AB与x轴重合时,有$\frac{1}{{E{A^2}}}+\frac{1}{{E{B^2}}}$=$\frac{12+2{x}_{0}^{2}}{(6-{x}_{0}^{2})^{2}}$,当直线AB与x轴垂直时,可得$\frac{1}{{E{A^2}}}+\frac{1}{{E{B^2}}}$=$\frac{6}{6-{x}_{0}^{2}}$,利用$\frac{{12+2{x_0}^2}}{{{{(6-{x_0}^2)}^2}}}=\frac{6}{{6-{x_0}^2}}$,解得x0,若存在点E,此时$E(±\sqrt{3},0)$,$\frac{1}{{E{A^2}}}+\frac{1}{{E{B^2}}}$为定值2.根据对称性,只需考虑直线AB过点$E(\sqrt{3},0)$,设A(x1,y1),B(x2,y2),又设直线AB的方程为$x=my+\sqrt{3}$,与椭圆C联立方程组,利用根与系数的关系即可得出.
解答 解:(1)由$\frac{c}{a}=\frac{{\sqrt{6}}}{3}$,设a=3k(k>0),则$c=\sqrt{6}k$,b2=3k2,
∴椭圆C的方程为$\frac{x^2}{{9{k^2}}}+\frac{y^2}{{3{k^2}}}=1$,
∵直线l垂直于x轴且点E为椭圆C的右焦点,即${x_A}={x_B}=\sqrt{6}k$,代入椭圆方程,解得y=±k,
于是$2k=\frac{{2\sqrt{6}}}{3}$,即$k=\frac{{\sqrt{6}}}{3}$,
∴椭圆C的方程为$\frac{x^2}{6}+\frac{y^2}{2}=1$.
(2)将$x=\sqrt{3}$代入$\frac{x^2}{6}+\frac{y^2}{2}=1$,解得y=±1,
∵点A在第一象限,从而$A(\sqrt{3},1)$,
由点E的坐标为$(\frac{{\sqrt{3}}}{2},0)$,∴${k_{AB}}=\frac{2}{{\sqrt{3}}}$,直线AB的方程为$y=\frac{2}{{\sqrt{3}}}(x-\frac{{\sqrt{3}}}{2})$,
联立$\left\{\begin{array}{l}{y=\frac{2}{\sqrt{3}}(x-\frac{\sqrt{3}}{2})}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,解得$B(-\frac{{\sqrt{3}}}{5},-\frac{7}{5})$,
又PA过原点O,于是$P(-\sqrt{3},-1)$,|PA|=4,
∴直线PA的方程为$x-\sqrt{3}y=0$,
∴点B到直线PA的距离$h=\frac{{|{-\frac{{\sqrt{3}}}{5}+\frac{{7\sqrt{3}}}{5}}|}}{2}=\frac{{3\sqrt{3}}}{5}$,
${S_{△PAB}}=\frac{1}{2}•4•\frac{{3\sqrt{3}}}{5}=\frac{{6\sqrt{3}}}{5}$.
(3)假设存在点E,使得$\frac{1}{{E{A^2}}}+\frac{1}{{E{B^2}}}$为定值,设E(x0,0),
当直线AB与x轴重合时,有$\frac{1}{{E{A^2}}}+\frac{1}{{E{B^2}}}=\frac{1}{{{{({x_0}+\sqrt{6})}^2}}}+\frac{1}{{{{(\sqrt{6}-{x_0})}^2}}}=\frac{{12+2{x_0}^2}}{{{{(6-{x_0}^2)}^2}}}$,
当直线AB与x轴垂直时,$\frac{1}{{E{A^2}}}+\frac{1}{{E{B^2}}}=\frac{2}{{2(1-\frac{{{x_0}^2}}{6})}}=\frac{6}{{6-{x_0}^2}}$,
由$\frac{{12+2{x_0}^2}}{{{{(6-{x_0}^2)}^2}}}=\frac{6}{{6-{x_0}^2}}$,解得${x_0}=±\sqrt{3}$,$\frac{6}{{6-{x_0}^2}}=2$,
∴若存在点E,此时$E(±\sqrt{3},0)$,$\frac{1}{{E{A^2}}}+\frac{1}{{E{B^2}}}$为定值2.
根据对称性,只需考虑直线AB过点$E(\sqrt{3},0)$,设A(x1,y1),B(x2,y2),
又设直线AB的方程为$x=my+\sqrt{3}$,与椭圆C联立方程组,
化简得$({m^2}+3){y^2}+2\sqrt{3}my-3=0$,
∴${y_1}+{y_2}=\frac{{-2\sqrt{3}m}}{{{m^2}+3}}$,${y_1}{y_2}=\frac{-3}{{{m^2}+3}}$,
又$\frac{1}{{E{A^2}}}=\frac{1}{{{{({x_1}-\sqrt{3})}^2}+{y_1}^2}}=\frac{1}{{{m^2}{y_1}^2+{y_1}^2}}=\frac{1}{{({m^2}+1){y_1}^2}}$,
∴$\frac{1}{{E{A^2}}}+\frac{1}{{E{B^2}}}=\frac{1}{{({m^2}+1){y_1}^2}}+\frac{1}{{({m^2}+1){y_2}^2}}=\frac{{{{({y_1}+{y_2})}^2}-2{y_1}{y_2}}}{{({m^2}+1){y_1}^2{y_2}^2}}$,
将上述关系代入,化简可得$\frac{1}{{E{A^2}}}+\frac{1}{{E{B^2}}}=2$.
综上所述,存在点$E(±\sqrt{3},0)$,使得$\frac{1}{{E{A^2}}}+\frac{1}{{E{B^2}}}$为定值2.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式,考查了分类讨论思想方法、探究能力、推理能力与计算能力,属于难题.

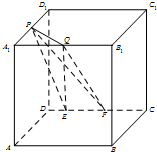 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )| A. | 点P到平面QEF的距离 | B. | 三棱锥P-QEF的体积 | ||
| C. | 直线PQ与平面PEF所成的角 | D. | 二面角P-EF-Q的大小 |
在一次篮球定点投篮训练中,规定每人最多投3次.在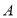 处每投进一球得3分;在
处每投进一球得3分;在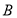 处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次. 某同学在
处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次. 某同学在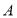 处的投中率
处的投中率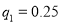 ,在
,在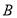 处的投中率为
处的投中率为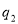 .该同学选择先在
.该同学选择先在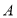 处投一球,以后都在
处投一球,以后都在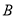 处投,且每次投篮都互不影响.用
处投,且每次投篮都互不影响.用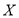 表示
表示
该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求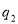 的值;
的值;
(2)求随机变量 的数学期望
的数学期望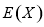 ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在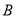 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.
 的公差为
的公差为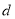 ,前
,前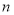 项和为
项和为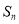 ,若
,若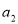 ,
,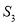 ,
,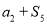 成等比数列,则
成等比数列,则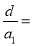 ( )
( )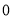 B.
B.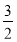
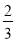 D.
D.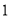
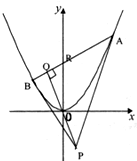 点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.
点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.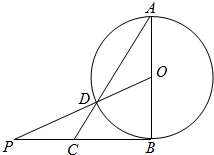 如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$.
如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$.