题目内容
20.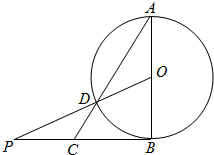 如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$.
如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$.
分析 连接BD,证明△PCD∽△PDB,求出PC,即可求出BC
解答 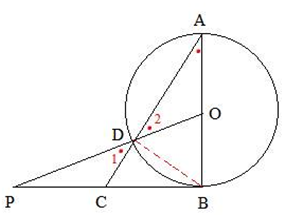 解:如图所示,连接BD,
解:如图所示,连接BD,
∵AB为⊙O的直径,
∴OA=OB=OD=$\frac{1}{2}$AB=1,
∵PB是⊙O的切线,
∴AB⊥PB,∠A=∠PBD,
∴OP=$\sqrt{O{B}^{2}+P{B}^{2}}$=3,
∴PD=OP-OD=2,
∵OA=OD,
∴∠A=∠2=∠1,
∴∠1=∠PBD,
∵∠P=∠P,
∴△PCD∽△PDB,
∴$\frac{PD}{PB}$=$\frac{PC}{PD}$,
∴PC=$\frac{P{D}^{2}}{PB}$=$\sqrt{2}$,
∴BC=PB-PC=$\sqrt{2}$,
故答案为:$\sqrt{2}$
点评 本题考查与圆有关的比例线段,考查三角形相似的证明,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.设实数x、y满足约束条件$\left\{\begin{array}{l}{3x-2y+4≥0}\\{x+y-4≤0}\\{x+ay-4≤0}\end{array}\right.$,已知z=2x+y的最大值是8,最小值是-5,则实数a的值为( )
| A. | 6 | B. | -6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |
9.过双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1 (a>0,b>0)的一个焦点F向其一条渐近线作垂线l,垂足为A,l与另一条渐近线交于B点,若$\overrightarrow{FB}=2\overrightarrow{FA}$,则双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
7.已知F是抛物线x2=4y的焦点,直线y=kx-1与该抛物线交于第一象限内的零点A,B,若|AF|=3|FB|,则k的值是( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
 值为___________.
值为___________.
 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.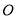 为极点,
为极点,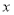 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 的极坐标为
的极坐标为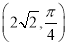 ,曲线
,曲线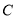 的参数方程为
的参数方程为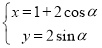 (
(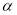 为参数).
为参数). 过
过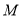 且与曲线
且与曲线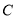 相切,求直线
相切,求直线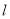 的极坐标方程;
的极坐标方程;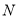 与点
与点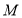 关于
关于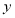 轴对称,求曲线
轴对称,求曲线 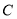 上的点到点
上的点到点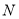 的距离的取值范围.
的距离的取值范围.