题目内容
【题目】选修4—5:不等式选讲
已知函数(x)=|2x-a|+ |x -1|.
（Ⅰ）当a=3时,求不等式(x)≥2的解集；
(Ⅱ)若(x)≥5-x对
恒成立,求实数a的取值范围.
【答案】(Ⅰ){x|x≤
或x≥2}.(Ⅱ)[6，+∞).
【解析】试题分析：(Ⅰ)
时，即求解
，分
三种情况，分别去掉绝对值得不等式的解集即可；(Ⅱ)根据题设条件得
恒成立，令
，再根据再根据数形结合可求得
的范围.
试题解析：(Ⅰ)当时,即求不等式的解集.
①当
时，
，解得
；
②当
时，
，解得
，此时无解；
③当
时, 
，解得
.
综上，原不等式的解集为
或
.
(Ⅱ)由题设得不等式对
恒成立.
令，作出函数
和
的图象(如图所示),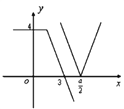 
则只需满足
，即
.
故所求实数的取值范围是
.
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
