��Ŀ����
����Ŀ����ij�����������ȡ10����ͥ����õ�i����ͥ��������xi(��λ��ǧԪ)���´���yi(��λ��ǧԪ)���������ϣ����![]() ��80��
��80�� ![]() ��20��
��20�� ![]() ��184��
��184�� ![]() ��720.
��720.
(1)���ͥ���´���y��������x�����Իع鷽��y��bx��a��
(2)�жϱ���x��y֮��������ػ��Ǹ���أ�
(3)���þ�����ij��ͥ������Ϊ7ǧԪ��Ԥ��ü�ͥ���´��
�������Իع鷽��y��bx��a�У�  ��a��
��a��![]() ��b
��b![]() ������
������![]() ��
�� ![]() Ϊ����ƽ��ֵ��
Ϊ����ƽ��ֵ��
���𰸡�(1) y��0.3x��0.4(2)�����(3) 1.7(ǧԪ)��
�����������������(1)�ȸ���������������������ĵ�����꣬�ٸ����������������ʽ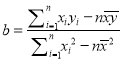 ����Ҫ���й������Ӷ��ɵõ�
����Ҫ���й������Ӷ��ɵõ�![]() ��ֵ�����������ĵ���������ع鷽�̼��ɵõ�
��ֵ�����������ĵ���������ع鷽�̼��ɵõ�![]() ��ֵ����������ûع鷽�̣���2��������ع鷽�̵�б�ʵ����������ж���������������ػ��Ǹ���أ���3��
��ֵ����������ûع鷽�̣���2��������ع鷽�̵�б�ʵ����������ж���������������ػ��Ǹ���أ���3��![]() ��������ع鷽�̿�Ԥ��ü�ͥ���´��
��������ع鷽�̿�Ԥ��ü�ͥ���´��
(1)������֪n��10�� ![]() ��
��![]() ��
��![]() ��8��
��8�� ![]() ��
��![]() ��
��![]() ��2.
��2.
��lxx��![]() ��n
��n![]() 2��720��10��82��80��
2��720��10��82��80��
lxy��![]() yi��n
yi��n![]()
![]() ��184��10��8��2��24.
��184��10��8��2��24.
�ɴ˵�b��![]() ��0.3��a��
��0.3��a��![]() ��b
��b![]() ��2��0.3��8����0.4��
��2��0.3��8����0.4��
������ع鷽��Ϊy��0.3x��0.4.
(2)���ڱ���y��ֵ��x��ֵ���Ӷ�����(b��0.3>0)����x��y֮��������أ�
(3)��x��7����ع鷽�̿���Ԥ��ü�ͥ���´���Ϊ
y��0.3��7��0.4��1.7(ǧԪ)��
���������硿������Ҫ�������Իع鷽�̼���Ӧ�ã���������.��ع�ֱ�߷��̵IJ��裺�������������ݻ���ɢ��ͼ��ȷ��������������������ع�ϵ���ڼ���![]() ��ֵ���ۼ���ع�ϵ��
��ֵ���ۼ���ع�ϵ��![]() ����д���ع�ֱ�߷���Ϊ
����д���ع�ֱ�߷���Ϊ![]() �� �ع�ֱ�߹�����������
�� �ع�ֱ�߹�����������![]() ��һ����Ҫ���ʣ��������Իع鷽�̿��Թ������壬�������Ƿ������������ı仯����.
��һ����Ҫ���ʣ��������Իع鷽�̿��Թ������壬�������Ƿ������������ı仯����.

 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�