题目内容
9.钝角△ABC的三个内角A、B、C的对边分别为a、b、c,A=$\frac{π}{4}$,sin2B+cos22C=1.(1)求角B,C;
(2)若a2+c2=b+$\sqrt{3}$ac+2,求a.
分析 (1)由题意可得C=$\frac{3π}{4}$-B,结合sin2B+cos22C=1可得cos2B的方程,解方程可得B,可得C;
(2)由a2+c2=b+$\sqrt{3}$ac+2和余弦定理可得b的方程b2-b-2=0,解方程可得b=2,再由正弦定理可得a值.
解答 解:(1)由题意可得B+C=π-A=$\frac{3π}{4}$,∴C=$\frac{3π}{4}$-B,
∵sin2B+cos22C=1,∴$\frac{1-cos2B}{2}$+$\frac{1+cos4C}{2}$=1,
∴cos4C=cos2B,即cos(3π-4B)=cos2B,
∴-cos4B=cos2B,∴2cos22B+2cos2B-1=0,
解得cos2B=-1,或cos2B=$\frac{1}{2}$,
当cos2B=-1时,2B=π可得B=$\frac{π}{2}$,这与△ABC为钝角三角形矛盾;
当cos2B=$\frac{1}{2}$时,2B=$\frac{π}{3}$可得B=$\frac{π}{6}$,符合题意,此时C=$\frac{7π}{12}$;
(2)∵a2+c2=b+$\sqrt{3}$ac+2,由余弦定理可得b2=a2+c2-2accosB,
∴a2+c2=b2+2accosB=b2+$\sqrt{3}$ac,∴b2+$\sqrt{3}$ac=b+$\sqrt{3}$ac+2,
整理可得b2-b-2=0,解得b=2,
由正弦定理可得a=$\frac{bsinA}{sinB}$=$\frac{2×\frac{\sqrt{2}}{2}}{\frac{1}{2}}$=2$\sqrt{2}$
点评 本题考查解三角形,涉及正余弦定理和二倍角公式,属中档题.

练习册系列答案
相关题目
18.执行下面的程序框图,那么输出的S等于( )
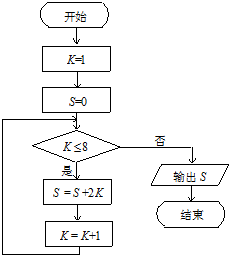

| A. | 42 | B. | 56 | C. | 72 | D. | 90 |
