题目内容
19.$\underset{lim}{x→∞}$$\frac{(2x-1)^{20}•(3x+2)^{30}}{(5x+1)^{50}}$=${(\frac{2}{5})}^{20}$•${(\frac{3}{5})}^{30}$.分析 把要求的式子进行变形,再利用数列极限的运算法则,求得结果.
解答 解:$\underset{lim}{x→∞}$$\frac{{(2x-1)}^{20}{•(3x+2)}^{30}}{{(5x+1)}^{50}}$=$\underset{lim}{x→∞}$$\frac{{(2-\frac{1}{x})}^{20}{•(3+\frac{2}{x})}^{30}}{{(5+\frac{1}{x})}^{50}}$=$\frac{{2}^{20}{•3}^{30}}{{5}^{50}}$=${(\frac{2}{5})}^{20}$•${(\frac{3}{5})}^{30}$,
故答案为:${(\frac{2}{5})}^{20}$•${(\frac{3}{5})}^{30}$.
点评 本题主要考查数列极限的运算法则的应用,式子的变形是解题的关键,属于基础题.

练习册系列答案
相关题目
14. 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=BA=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=BA=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.
(Ⅰ)求证:平面ABC⊥平面ABB1A1;
(Ⅱ)求B到平面AB1D的距离.
 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=BA=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=BA=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.(Ⅰ)求证:平面ABC⊥平面ABB1A1;
(Ⅱ)求B到平面AB1D的距离.
8.如图所示,正弦曲线y=sinx,余弦曲线y=cosx与两直线x=0,x=π所围成的阴影部分的面积为( )


| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |

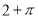 B.
B.
 D.
D.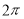
 已知棱长为2的正方体ABCD-GPHF截去一个多面体后,所得几何体如图所示,点E在GP上,且EG=1.
已知棱长为2的正方体ABCD-GPHF截去一个多面体后,所得几何体如图所示,点E在GP上,且EG=1. 若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.
若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.