题目内容
14.已知等比数列{an}的公比q>1,前n项和为Sn,S3=7,且a1+3,3a2,a3+4成等差数列,数列{bn}满足关系式bn(3n-5)=bn-1(3n-2)其中n≥2,n∈N+,且b1=1.(1)求数列{an}及{bn}的通项公式;
(2)设A={a1,a2,…a10},B={b1,b2,…b50},C=A∪B,求集合C中所有元素之和.
分析 (1)由条件利用等差数列、等比数列的定义和性质求出首项和公差、公比,从而求得数列{an}及{bn}的通项公式.
(2)哟条件利用前n项和公式求得等比数列{an}的前10项和S10、等差数列{bn}前50项和 T50 的值,再求得A与B的公共元素的和,从而求得集合C中所有元素之和.
解答 解:(1)因为S3=7,∴a1+a2 +a3=7.
因为a1+3,3a2,a3+4成等差数列,所以,a1+3,+a3+4=6a2 ,求得a2 =a1•q=2 ①.
又由a1+a2 +a3=7得a1 +a1•q2=5 ②,
由①②可得 2q2-5q+2=0,解得q=2,或q=$\frac{1}{2}$(舍去),∴a1=1,an =2n-1.
另由于{bn}满足关系式bn(3n-5)=bn-1(3n-2),即 $\frac{{b}_{n}}{{b}_{n-1}}$=$\frac{3n-2}{3n-5}$.
所以由累乘法得 $\frac{{b}_{n}}{{b}_{1}}$=3n-2,而b1=1,所以 bn=3n-2 (n≥2),当n=1时也满足,
故bn=3n-2.
(2)等比数列{an}的前n项和为Sn,则 S10=$\frac{1{-2}^{10}}{1-2}$=1023.
等差数列{bn}前n项和为Tn,则 T50=$\frac{50×(1+148)}{2}$=3725,
因为A与B的公共元素有1,4,16,64,其和为85,
所以集合C中所有元素之和为1023+3725-85=4663.
点评 本题主要考查等差数列及等比数列的定义、性质、通项公式,前n项和公式的应用,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
2.某高中采取分层抽样的方法从应届高二学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
(1)若在该样本中从报考文科的男生和报考理科的女生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(2)用独立性检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关?(参考公式和数据:χ2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$(其中n=a+b+c+d))
| 性别 科目 | 男 | 女 |
| 文科 | 2 | 5 |
| 理科 | 10 | 3 |
(2)用独立性检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关?(参考公式和数据:χ2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$(其中n=a+b+c+d))
9.钝角△ABC的三个内角A、B、C的对边分别为a、b、c,A=$\frac{π}{4}$,sin2B+cos22C=1.
(1)求角B,C;
(2)若a2+c2=b+$\sqrt{3}$ac+2,求a.
(1)求角B,C;
(2)若a2+c2=b+$\sqrt{3}$ac+2,求a.
19.某设备的使用年限x(单位:年)与所支付的维修费用y(单位:千元)的一组数据如表:
从散点图分析.y与x线性相关,根据上表中数据可得其线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{b}$=1.54.由此预测该设备的使用年限为6年时需支付的维修费用约是( )
| 使用年限x | 2 | 3 | 4 | 5 |
| 维修费用y | 2 | 3.4 | 5 | 6.6 |
| A. | 7.2千元 | B. | 7.8千元 | C. | 8.1千元 | D. | 9.5千元 |
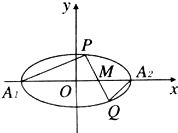 若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.
若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.