题目内容
14.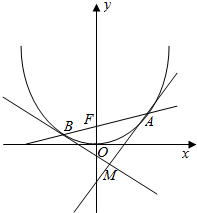 如图所示,已知过抛物线x2=2py(p>0)的焦点F的直线l与抛物线相交于A,B两点
如图所示,已知过抛物线x2=2py(p>0)的焦点F的直线l与抛物线相交于A,B两点(1)若A(x1,3)到焦点F的距离为4,求抛物线的方程;
(2)若抛物线方程为x2=4y,在A,B两点处的切线相交于点M,若点M的横坐标为2,求△ABM的外接圆方程.
分析 (1)利用抛物线的定义求出p,即可求抛物线的方程;
(2)设直线AB的方程为y=kx+1,A(x1,y1),B(x2,y2).与抛物线方程联立化为x2-4kx-4=0,可得根与系数的关系,由x2=4y,可得y′=$\frac{1}{2}$x.可得kMA•kMB=$\frac{{x}_{1}{x}_{2}}{4}$=-1,可得△MAB为直角三角形,可得△MAB的外接圆的圆心为线段AB的中点.设线段AB的中点为P,可得⊙P与抛物线的准线相切,切点为点M,利用中点坐标公式与根与系数的关系可得圆心P(2,3),半径r=|MP|=|3-(-1)|=4,即可得出所求的△MAB的外接圆的方程.
解答 解:(1)抛物线x2=2py的准线方程为y=-$\frac{p}{2}$,
∵A(x1,3)到焦点F的距离为4,
∴3+$\frac{p}{2}$=4,
∴p=2,
∴抛物线的方程为x2=4y;
(2)设直线AB的方程为y=kx+1,A(x1,y1),B(x2,y2).
代入x2=4y,化为x2-4kx-4=0,
∴x1+x2=4k,x1x2=-4.
由x2=4y,可得y′=$\frac{1}{2}$x.
∴kMA•kMB=$\frac{{x}_{1}{x}_{2}}{4}$=-1,
∴MA⊥MB.
∴△MAB为直角三角形,∴△MAB的外接圆的圆心为线段AB的中点.
设线段AB的中点为P,可得⊙P与抛物线的准线相切,切点为点M.
∴xP=xM=2,
∴$\frac{{x}_{1}+{x}_{2}}{2}$=2,2k=2,解得k=1.
yp=$\frac{{x}_{1}+{x}_{2}+2}{2}$=3,
∴圆心P(2,3),又r=|MP|=|3-(-1)|=4,
∴所求的△MAB的外接圆的方程为:(x-2)2+(y-3)2=16.
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题转化为方程联立可得根与系数的关系,考查了推理能力与计算能力,属于中档题.

| 学生编号i | 1 | 2 | 3 | 4 | 5 |
| 体能成绩x | 80 | 75 | 70 | 65 | 60 |
| 心理成绩y | 70 | 66 | 68 | 64 | 62 |
(2)假设学生的体能成绩和心理成绩具有线性相关关系,根据上表利用最小二乘法,求y与x的回归直线方程,(参考数据:$\underset{\stackrel{5}{∑}}{i=1}$xiyi=23190,$\underset{\stackrel{5}{∑}}{i=1}$xi2=24750).
| A. | (1,+∞) | B. | (0,1) | C. | (-1,1) | D. | (-∞,1) |
 如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积为( )
如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积为( )| A. | 2+$\sqrt{2}$ | B. | $\frac{{1+\sqrt{2}}}{2}$ | C. | $\frac{{2+\sqrt{2}}}{2}$ | D. | 1+$\sqrt{2}$ |