题目内容
9.说明下列极坐标方程表示什么曲线,并画圆.(1)ρ=$\frac{π}{3}$;
(2)ρcosθ=2;
(3)ρ=3;
(4)ρ=6cosθ;
(5)ρ=10sinθ.
分析 利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,ρ2=x2+y2即可化为直角坐标方程.
解答 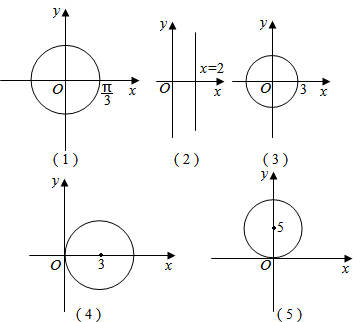 解:(1)ρ=$\frac{π}{3}$,表示圆:x2+y2=$\frac{{π}^{2}}{9}$;
解:(1)ρ=$\frac{π}{3}$,表示圆:x2+y2=$\frac{{π}^{2}}{9}$;
(2)ρcosθ=2,表示直线x=2;
(3)ρ=3表示圆:x2+y2=9;
(4)ρ=6cosθ,化为ρ2=6ρcosθ,即x2+y2=6x,配方为(x-3)2+y2=9,表示以(3,0)为圆,3为半径的圆;
(5)ρ=10sinθ,化为ρ2=10ρsinθ,
即x2+y2=10y,配方为x2+(y-5)2=25,表示以(0,5)为圆,5为半径的圆.
点评 本题考查了极坐标方程化为直角坐标方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.某校为了选拔学生参加体育比赛,对5名学生的体能和心理进行了测评,成绩(单位:分)如下表:
(1)在本次测评中,规定体能成绩70分以上(含70分)且心理成绩65分以上(含65分)为优秀成绩,从这5名学生中任意抽取2名学生,设X表示成绩优秀的学生人数,求X的分布列和数学期望;
(2)假设学生的体能成绩和心理成绩具有线性相关关系,根据上表利用最小二乘法,求y与x的回归直线方程,(参考数据:$\underset{\stackrel{5}{∑}}{i=1}$xiyi=23190,$\underset{\stackrel{5}{∑}}{i=1}$xi2=24750).
| 学生编号i | 1 | 2 | 3 | 4 | 5 |
| 体能成绩x | 80 | 75 | 70 | 65 | 60 |
| 心理成绩y | 70 | 66 | 68 | 64 | 62 |
(2)假设学生的体能成绩和心理成绩具有线性相关关系,根据上表利用最小二乘法,求y与x的回归直线方程,(参考数据:$\underset{\stackrel{5}{∑}}{i=1}$xiyi=23190,$\underset{\stackrel{5}{∑}}{i=1}$xi2=24750).