题目内容
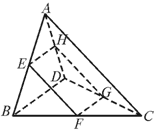
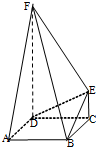
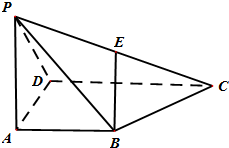
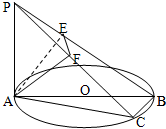
如图,在边长为4的菱形ABCD中,∠DAB=60°.点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O.沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.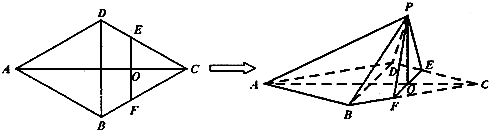
(Ⅰ)求证:BD⊥平面POA;
(Ⅱ)记三棱锥P-ABD体积为V1,四棱锥P-BDEF体积为V2.求当PB取得最小值时的V1:V2值.

(Ⅰ)求证:BD⊥平面POA;
(Ⅱ)记三棱锥P-ABD体积为V1,四棱锥P-BDEF体积为V2.求当PB取得最小值时的V1:V2值.
(Ⅰ)证明:在菱形ABCD中,∵BD⊥AC,∴BD⊥AO.
∵EF⊥AC,∴PO⊥EF,
∵平面PEF⊥平面ABFED,平面PEF∩平面ABFED=EF,且PO?平面PEF,
∴PO⊥平面ABFED,
∵BD?平面QBFED,∴PO⊥BD.
∵AO∩PO=O,所以BD⊥平面POA.
(Ⅱ)连接OB,设AO∩BD=H.
由(Ⅰ)知,AC⊥BD.
∵∠DAB=60°,BC=4,
∴BH=2,CH=2
.
设OH=x(0<x<2
).
由(Ⅰ)知,PO⊥平面ABFED,故△POB为直角三角形.
∴PB2=OB2+PO2=(BH2+OH2)+PO2,
∴PB2=2(x-
)2+10.
当x=
时,PB取得最小值,此时O为CH中点.
∴S△CEF=
S△BCD,
∴S梯形BDEF=
S△BCD=
S△ABD,
∴
=
=
∴当PB取得最小值时,V1:V2的值为4:3.
∵EF⊥AC,∴PO⊥EF,
∵平面PEF⊥平面ABFED,平面PEF∩平面ABFED=EF,且PO?平面PEF,
∴PO⊥平面ABFED,
∵BD?平面QBFED,∴PO⊥BD.
∵AO∩PO=O,所以BD⊥平面POA.
(Ⅱ)连接OB,设AO∩BD=H.
由(Ⅰ)知,AC⊥BD.
∵∠DAB=60°,BC=4,
∴BH=2,CH=2
| 3 |
设OH=x(0<x<2
| 3 |
由(Ⅰ)知,PO⊥平面ABFED,故△POB为直角三角形.
∴PB2=OB2+PO2=(BH2+OH2)+PO2,
∴PB2=2(x-
| 3 |
当x=
| 3 |
∴S△CEF=
| 1 |
| 4 |
∴S梯形BDEF=
| 3 |
| 4 |
| 3 |
| 4 |
∴
| V1 |
| V2 |
| S△ABD |
| S梯形BDEF |
| 4 |
| 3 |
∴当PB取得最小值时,V1:V2的值为4:3.

练习册系列答案
相关题目