题目内容
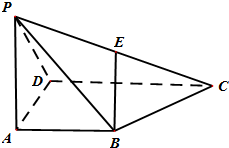
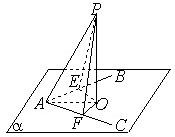
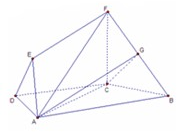
如图,在梯形ABCD中,AB∥C,AD=DC=CB=1,∠ABC═60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
(1)求证:BC⊥平面ACFE;
(2)求二面角A-BF-C的平面角的余弦值;
(3)若点M在线段EF上运动,设平MAB与平FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.
(1)求证:BC⊥平面ACFE;
(2)求二面角A-BF-C的平面角的余弦值;
(3)若点M在线段EF上运动,设平MAB与平FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.

(1)证明:在梯形ABCD中,∵AB∥CD,AD=DC=CB=1,∠ABC=60°,
∴AB=2,AC2=AB2+BC2-2AB•BC•cos60°=3,
∴AB2=AC2+BC2,∴BC⊥AC,
∵平面ACFE⊥平面ABCD,
平面ACFE∩平面ABCD=AC,BC?平面ABCD,
∴BC⊥平面ACFE.
(2)取FB中点G,连接AG,CG,
∵AF=
=2,∴AB=AF,∴AG⊥FB,
∵CF=CB=1,∴CG⊥FB,∴∠AGC=θ,
∵BC=CF,∴FB=
,∴CG=
,AG=
,
∴cosθ=
=
.
(3)由(2)知:
①当M与F重合时,cosθ=
.
②当M与E重合时,过B作BN∥CF,且使BN=CF,
连接EN,FN,则平面MAB∩平面FCB,
∵BC⊥CF,AC⊥CF,∴CF⊥平面ABC,∴BN⊥平面ABC,
∴∠ABC=θ,∴θ=60°,∴cosθ=
.
③当M与E,F都不重合时,令FM=λ,0<λ<
,
延长AM交CF的延长线于N,连接BN,
∴N在平面MAB与平面FCB的交线上,
∵B在平面MAB与平面FCB的交线上,
∴平面MAB∩平面FCB=BN,
过C作CH⊥NB交NB于H,连接AH,
由(1)知,AC⊥BC,
又∵AC⊥CN,∴AC⊥平面NCB,∴AC⊥NB,
又∵CH⊥NB,AC∩CH=C,∴NB⊥平面ACH,
∴AH⊥NB,∴∠AHC=θ,
在△NAC中,NC=
,
从而在△NCB中,CH=
,
∵∠ACH=90°,∴AH=
=
,
∴cosθ=
=
,
∵0<λ<
,
∴
<cosθ<
,
综上所述,cosθ∈[
,
].
∴AB=2,AC2=AB2+BC2-2AB•BC•cos60°=3,
∴AB2=AC2+BC2,∴BC⊥AC,
∵平面ACFE⊥平面ABCD,
平面ACFE∩平面ABCD=AC,BC?平面ABCD,
∴BC⊥平面ACFE.
(2)取FB中点G,连接AG,CG,
∵AF=
| AC2+CF2 |
∵CF=CB=1,∴CG⊥FB,∴∠AGC=θ,
∵BC=CF,∴FB=
| 2 |
| ||
| 2 |
| ||
| 2 |
∴cosθ=
| CG2+AG2-AC2 |
| 2CG•AG |
| ||
| 7 |

(3)由(2)知:
①当M与F重合时,cosθ=
| ||
| 7 |
②当M与E重合时,过B作BN∥CF,且使BN=CF,
连接EN,FN,则平面MAB∩平面FCB,
∵BC⊥CF,AC⊥CF,∴CF⊥平面ABC,∴BN⊥平面ABC,
∴∠ABC=θ,∴θ=60°,∴cosθ=
| 1 |
| 2 |
③当M与E,F都不重合时,令FM=λ,0<λ<
| 3 |
延长AM交CF的延长线于N,连接BN,
∴N在平面MAB与平面FCB的交线上,
∵B在平面MAB与平面FCB的交线上,
∴平面MAB∩平面FCB=BN,
过C作CH⊥NB交NB于H,连接AH,

由(1)知,AC⊥BC,
又∵AC⊥CN,∴AC⊥平面NCB,∴AC⊥NB,
又∵CH⊥NB,AC∩CH=C,∴NB⊥平面ACH,
∴AH⊥NB,∴∠AHC=θ,
在△NAC中,NC=
| ||
|
从而在△NCB中,CH=
| ||
(λ-
|
∵∠ACH=90°,∴AH=
| AC2+CH2 |
| ||||||
|
∴cosθ=
| CH |
| AH |
| 1 | ||||
|
∵0<λ<
| 3 |
∴
| ||
| 7 |
| 1 |
| 2 |
综上所述,cosθ∈[
| ||
| 7 |
| 1 |
| 2 |

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目