题目内容
(本小题满分14分)已知递增数列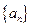 满足:
满足: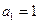 ,
,
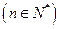 ,且
,且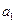 、
、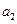 、
、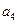 成等比数列。(I)求数列
成等比数列。(I)求数列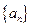 的通项公式
的通项公式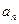 ;(II)若数列
;(II)若数列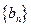 满足:
满足:
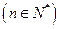 ,且
,且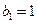 。①证明数列
。①证明数列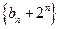 是等比数列,并求数列
是等比数列,并求数列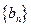 的通项公式
的通项公式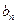 ;②设
;②设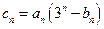 ,数列
,数列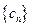 前
前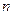 项和为
项和为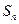 ,
,
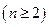 ,
,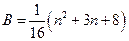 。当
。当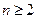 时,试比较A与B的大小。
时,试比较A与B的大小。
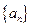 满足:
满足: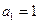 ,
,
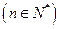 ,且
,且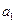 、
、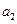 、
、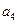 成等比数列。(I)求数列
成等比数列。(I)求数列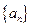 的通项公式
的通项公式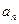 ;(II)若数列
;(II)若数列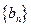 满足:
满足:
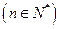 ,且
,且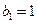 。①证明数列
。①证明数列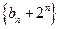 是等比数列,并求数列
是等比数列,并求数列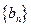 的通项公式
的通项公式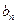 ;②设
;②设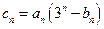 ,数列
,数列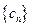 前
前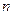 项和为
项和为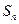 ,
,
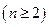 ,
,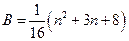 。当
。当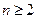 时,试比较A与B的大小。
时,试比较A与B的大小。(Ⅰ)  (Ⅱ) (Ⅲ)
(Ⅱ) (Ⅲ)
 (Ⅱ) (Ⅲ)
(Ⅱ) (Ⅲ)(1) ,∴数列
,∴数列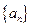 为等差数列,设公差为
为等差数列,设公差为
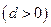 。
。
 、
、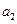 、
、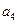 成等比数列,∴
成等比数列,∴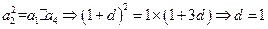
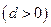
 4分
4分
(2)①证明:

∴数列{ }的公比为3,首项为
}的公比为3,首项为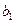 +2=3的等比数列。
+2=3的等比数列。
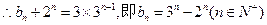 ………4分
………4分
②由题意, ∴
∴

相减得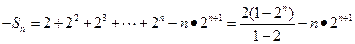




∴当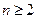 时,
时, 。 ………6分
。 ………6分
 ,∴数列
,∴数列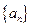 为等差数列,设公差为
为等差数列,设公差为
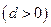 。
。 、
、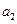 、
、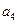 成等比数列,∴
成等比数列,∴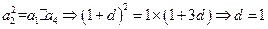
 4分
4分(2)①证明:


∴数列{
 }的公比为3,首项为
}的公比为3,首项为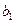 +2=3的等比数列。
+2=3的等比数列。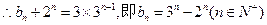 ………4分
………4分②由题意,
 ∴
∴

相减得
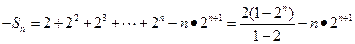




∴当
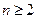 时,
时, 。 ………6分
。 ………6分
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 }的前n项和记为Sn.已知
}的前n项和记为Sn.已知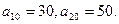 (Ⅰ)求通项
(Ⅰ)求通项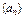 满足
满足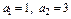 ,且
,且 。
。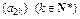 为等比数列;(2)求数列
为等比数列;(2)求数列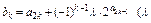 为非零常数)。试确定
为非零常数)。试确定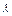 的值,使得对任意
的值,使得对任意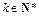 都有
都有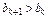 成立。
成立。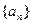 的首项为a1,公比q为正数(q≠1)的等比数列,其前n项和为Sn,且
的首项为a1,公比q为正数(q≠1)的等比数列,其前n项和为Sn,且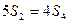 . (1)求q的值; (2)设
. (1)求q的值; (2)设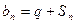 ,请判断数列
,请判断数列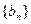 能否为等比数列,若能,请求出a1的值,否则请说明理由.
能否为等比数列,若能,请求出a1的值,否则请说明理由.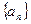 与等比数列
与等比数列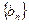 满足:
满足: ,
,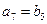 那么( )
那么( ) 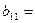
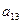
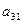
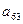
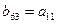
 中,
中, ,那么
,那么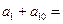 .
.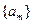 的前
的前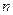 项和为
项和为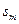 .若
.若 .
.