题目内容
【题目】对某地区儿童的身高与体重的一组数据,我们用两种模型①![]() ,②
,②![]() 拟合,得到回归方程分别为
拟合,得到回归方程分别为![]() ,
, ![]() ,作残差分析,如表:
,作残差分析,如表:
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
体重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于![]() 的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为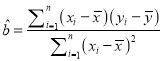 ,
, ![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)模型①的拟合效果比较好;(Ⅲ)
;(Ⅱ)模型①的拟合效果比较好;(Ⅲ) ![]() .
.
【解析】试题分析:(Ⅰ)将![]() 代入相应回归方程,再做差即可;(Ⅱ)比较模型①残差的绝对值与模型②残差的绝对值和即可的结论;(Ⅲ)直接根据公式
代入相应回归方程,再做差即可;(Ⅱ)比较模型①残差的绝对值与模型②残差的绝对值和即可的结论;(Ⅲ)直接根据公式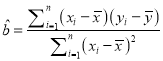 求出
求出![]() 的值,将样本的中心点代入方程可得
的值,将样本的中心点代入方程可得![]() 的值,进而得结果.
的值,进而得结果.
试题解析:(Ⅰ)根据残差分析,把![]() 代入
代入![]() 得
得![]() .
.
![]() .所以表中空格内的值为
.所以表中空格内的值为![]() .
.
(Ⅱ)模型①残差的绝对值和为![]() ,
,
模型②残差的绝对值和为![]() .
.
![]() ,所以模型①的拟合效果比较好,选择模型①.
,所以模型①的拟合效果比较好,选择模型①.
(Ⅲ)残差大于![]() 的样本点被剔除后,剩余的数据如表
的样本点被剔除后,剩余的数据如表
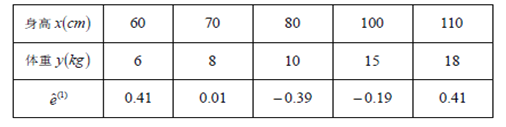
由公式: 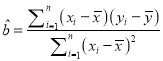 ,
, ![]() .得回归方程为
.得回归方程为![]() .
.

【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在![]() 内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
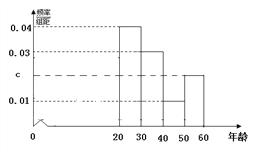
(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.