题目内容
【题目】若不等式x2+ax+1≥0对一切x∈（0， 
]成立，则a的最小值是 ．
【答案】-2
【解析】解：不等式x2+ax+1≥0对一切x∈（0， 
]成立，
∴ax≥﹣x2﹣1，
即a≥﹣x﹣ 
=﹣（x+ ）；
由x∈（0， ]，
∴x+ ≥2 
=2，当且仅当x=1时“=”成立，
即﹣（x+ ）的最大值是﹣2；
∴a的最小值是﹣2．
所以答案是：﹣2．
【考点精析】掌握解一元二次不等式是解答本题的根本，需要知道求一元二次不等式
解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边．
练习册系列答案
相关题目
【题目】对某地区儿童的身高与体重的一组数据，我们用两种模型①
，②
拟合，得到回归方程分别为
， 
，作残差分析，如表：
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
体重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | －0.19 | 0.41 | |
| －0.36 | 0.07 | 0.12 | 1.69 | －0.34 | －1.12 |
（Ⅰ）求表中空格内的值；
（Ⅱ）根据残差比较模型①，②的拟合效果，决定选择哪个模型；
（Ⅲ）残差大于
的样本点被认为是异常数据，应剔除，剔除后对(Ⅱ)所选择的模型重新建立回归方程.
（结果保留到小数点后两位）
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘法估计分别为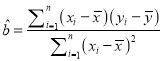
， 
.
