题目内容
【题目】某市为了宣传环保知识，举办了一次“环保知识知多少”的问卷调查活动（一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份， 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
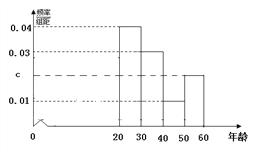
（1）分别求出n， a， b， c的值；
（2）从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”，求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.
【答案】（1）
；（2）
.
【解析】试题分析：（1）根据频率直方分布图，通过概率的和为1，求求出n，a，b，c的值，
（2）年龄在[40，50）中答对全卷的4人记为A，B，C，D，年龄在[50，60]中答对全卷的2人记为a，b，分别列举出所有的基本事件，根据概率公式计算即可．
试题解析：
（1）因为抽取总问卷为100份，所以n=100-(40+10+20)=30.
年龄在
中，抽取份数为10份，答对全卷人数为4人，所以b=
=0.4.
年龄在
中，抽取份数为20份，答对全卷人数占本组的概率为0.1，所以
=0.1，得
.
根据频率直方分布图，得(0.04+0.03+c+0.01)×10=1，解得
.
（2）因为年龄在
与
中答对全卷的人数分别为4人与2人．
年龄在
中答对全卷的4人记为
， 
， 
， 
，年龄在中答对全卷的2人记为
， 
，则从这6人中随机抽取2人授予“环保之星”奖的所有可能的情况是： 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
,共15种(8分)．
其中所抽取年龄在的人中至少有1人被授予“环保之星”的情况是： 
， 
， 
， 
， 
， 
， 
， 
， 
共9种．
故所求的概率为
.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】对某地区儿童的身高与体重的一组数据，我们用两种模型①
，②
拟合，得到回归方程分别为
， 
，作残差分析，如表：
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
体重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | －0.19 | 0.41 | |
| －0.36 | 0.07 | 0.12 | 1.69 | －0.34 | －1.12 |
（Ⅰ）求表中空格内的值；
（Ⅱ）根据残差比较模型①，②的拟合效果，决定选择哪个模型；
（Ⅲ）残差大于
的样本点被认为是异常数据，应剔除，剔除后对(Ⅱ)所选择的模型重新建立回归方程.
（结果保留到小数点后两位）
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘法估计分别为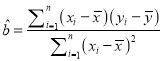
， 
.
