题目内容
【题目】已知函数![]() 对一切实数
对一切实数![]() 都有
都有![]()
![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)已知![]() ,设
,设![]() :当
:当![]() 时,不等式
时,不等式![]() 恒成立;Q:当
恒成立;Q:当![]() 时,
时,![]() 是单调函数。如果满足
是单调函数。如果满足![]() 成立的
成立的![]() 的集合记为
的集合记为![]() ,满足Q成立的
,满足Q成立的![]() 的集合记为
的集合记为![]() ,求A∩(CRB)(
,求A∩(CRB)(![]() 为全集).
为全集).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)对抽象函数满足的函数值关系的理解和把握是解决该问题的关键,对自变量适当的赋值可以解决该问题,结合已知条件可以赋![]() 求出
求出![]() ;(2)在(1)基础上赋值
;(2)在(1)基础上赋值![]() 可以实现求解
可以实现求解![]() 的解析式的问题;(3)利用(2)中求得的函数的解析式,结合恒成立问题的求解策略,即转化为相应的二次函数最值问题求出集合
的解析式的问题;(3)利用(2)中求得的函数的解析式,结合恒成立问题的求解策略,即转化为相应的二次函数最值问题求出集合![]() ,利用二次函数的单调性求解策略求出集合
,利用二次函数的单调性求解策略求出集合![]() .
.
试题解析:(1)令x=﹣1,y=1,则由已知f(0)﹣f(1)=﹣1(﹣1+2+1)
∴f(0)=﹣2
(2)令y=0,则f(x)﹣f(0)=x(x+1)
又∵f(0)=﹣2,∴f(x)=x2+x﹣2
(3)不等式f(x)+3<2x+a即x2+x﹣2+3<2x+a
也就是x2﹣x+1<a.由于当![]() 时,
时,![]() ,
,
又x2﹣x+1=![]() 恒成立,
恒成立,
故A={a|a≥1},g(x)=x2+x﹣2﹣ax=x2+(1﹣a)x﹣2 对称轴x=![]() ,
,
又g(x)在[﹣2,2]上是单调函数,故有![]() ,或
,或![]() ,
,
∴B={a|a≤﹣3,或a≥5},CRB={a|﹣3<a<5},∴A∩CRB={a|1≤a<5}.

【题目】对某地区儿童的身高与体重的一组数据,我们用两种模型①![]() ,②
,②![]() 拟合,得到回归方程分别为
拟合,得到回归方程分别为![]() ,
, ![]() ,作残差分析,如表:
,作残差分析,如表:
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
体重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于![]() 的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为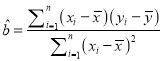 ,
, ![]() .
.