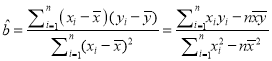题目内容
【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且满足 
acosC﹣csinA=0．
（1）求角C的大小；
（2）已知b=4，△ABC的面积为6 ，求边长c的值．
【答案】
（1）解：在△ABC中，由正弦定理得： 
sinAcosC﹣sinCsinA=0． …（2分）
因为0＜A＜π，所以sinA＞0，
从而 cosC=sinC，又cosC≠0，
所以tanC= ，所以C= 
．
（2）解：在△ABC中，S△ABC= 
=6 ，得a=6，
由余弦定理得：c2=62+42﹣2× 
=28，
所以c=2 
【解析】（1）由正弦定理得： sinAcosC﹣sinCsinA=0，即可解得tanC= ，从而求得C的值；（2）由面积公式可得S△ABC= =6 ，从而求得得a的值，由余弦定理即可求c的值．
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识，掌握正弦定理:
，以及对余弦定理的定义的理解，了解余弦定理:
;
;
．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
