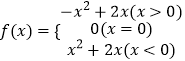题目内容
【题目】已知函数f(x)=x(1+m|x|),关于x的不等式f(x)>f(x+m)的解集记为T,若区间[﹣ ![]() ,
, ![]() ]T,则实数m的取值范围是( )
]T,则实数m的取值范围是( )
A.( ![]() ,0)
,0)
B.( ![]() ,0)
,0)
C.(﹣∞, ![]() )
)
D.( ![]() ,0)∪(0,
,0)∪(0, ![]() )
)
【答案】A
【解析】解:f(x)=x(1+m|x|)= ![]() ,
,
①若m=0,则不等式即f(x)>f(x ),显然不成立.
②若m>0,函数f(x)= ![]() ,在R上是增函数,如右图所示:
,在R上是增函数,如右图所示:
由f(x)>f(x+m),可得x>x+m,m<0,故m无解.
③若m<0,函数y=f(x+m)的图象是把函数y=f(x)的图象向右平移﹣m个单位得到的,
由题意可得,当x∈[﹣ ![]() ,
, ![]() ]时,函数y=f(x+m)的图象在函数 y=f(x)的图象的下方,
]时,函数y=f(x+m)的图象在函数 y=f(x)的图象的下方,
如下图所示: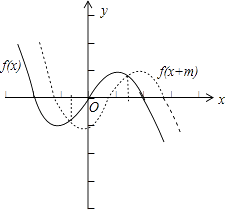
只要f(﹣ ![]() ﹣m)<f(﹣
﹣m)<f(﹣ ![]() )即可,
)即可,
即m(﹣ ![]() ﹣m)2+(﹣
﹣m)2+(﹣ ![]() ﹣m)<﹣m(﹣
﹣m)<﹣m(﹣ ![]() )2﹣
)2﹣ ![]() ,
,
即 m2﹣m﹣1<0,求得 ![]() <m<
<m< ![]() ,
,
综合可得, ![]() <m<0,
<m<0,
故选:A.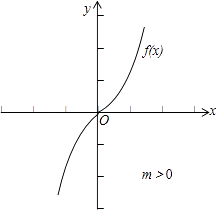

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目