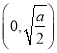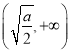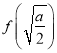题目内容
【题目】已知函数![]() (
(![]() ),
),![]() (
(![]() ).
).
(1)讨论![]() 的单调性;
的单调性;
(2)设![]() ,
, ![]() ,若
,若![]() (
(![]() )是
)是![]() 的两个零点,且
的两个零点,且![]() ,
,
试问曲线![]() 在点
在点![]() 处的切线能否与
处的切线能否与![]() 轴平行?请说明理由.
轴平行?请说明理由.
【答案】(1)当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 单调递增,
单调递增, 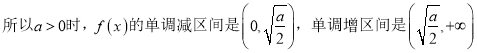 ;(2)
;(2)![]() 在
在![]() 处的切线不能平行于
处的切线不能平行于![]() 轴. 。
轴. 。
【解析】试题分析:(1)先对函数求导,再依据到函数值与函数单调性之间的关系分类探求单调区间;(2)先假设曲线![]() 在点
在点![]() 处的切线能否与
处的切线能否与![]() 轴平行,然后依据假设建立方程组,最后再构造函数
轴平行,然后依据假设建立方程组,最后再构造函数![]() 运用导数的知识断定假设不成立。
运用导数的知识断定假设不成立。
解:(Ⅰ) ![]()
(1)当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 单调递增,
单调递增,
(2)当![]() 时,
时, ![]() 有
有
|
|
|
|
| - | 0 | + |
| ↘ | 极小值 | ↗ |
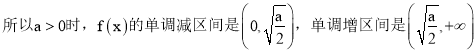
(Ⅱ) ![]()
假设![]() 在
在![]() 处的切线能平行于
处的切线能平行于![]() 轴.
轴.
∵![]()
由假设及题意得:
![]() .................
.................
![]() ................
................
![]() .................
.................
![]() .............④
.............④
由-得, ![]()
即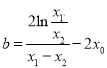 .................⑤
.................⑤
由④⑤得, 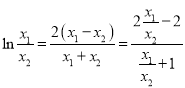
令![]() ,
, ![]() .则上式可化为
.则上式可化为![]() ,
,
设函数![]() ,则
,则
 ,
,
所以函数![]() 在
在![]() 上单调递增.
上单调递增.
于是,当![]() 时,有
时,有![]() ,即
,即![]() 与⑥矛盾.
与⑥矛盾.
所以![]() 在
在![]() 处的切线不能平行于
处的切线不能平行于![]() 轴.
轴.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目