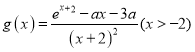Question

【题目】已知函数.

（Ⅰ）若过点恰有两条直线与曲线相切，求的值；

（Ⅱ）用表示中的最小值，设函数，若恰有三个零点，求实数的取值范围.

Answer 1

【答案】（Ⅰ）;（Ⅱ）.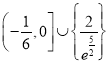

【解析】试题分析：（Ⅰ）求导，利用导数求得 的过点的切线方程，构造辅助函数，利用导数与函数单调性的关系，分类讨论即可得a的值;

（Ⅱ）根据函数的定义求，根据函数的单调性及零点的判断，采用分类讨论法，求得函数零点的个数，即可求得恰有三个零点，求实数的取值范围.

试题解析：（Ⅰ）∵，∴，

设切点为，则该点处的切线方程为，

又∵切线过点，∴，

整理得， ，（*）

依题设，方程（*）恰有两个不同的解，

令，则，

解得，

①当时， 恒成立， 单调递增，至多只有一个零点，不合题设；

②当时，则为的极值点，若恰有两个不同的解，

则或，又∵，

，∴或.

令，则，

解得，∴在上单调递增，在上单调递减，

又∵， ∴当且时， 无解. ∴.

（Ⅱ）∵，

∴当时，解得.

由（Ⅰ）知， ，

当时， ；当或时， ，

∴在上单调递增，在上单调递减.

∴当时， ，当时， .

∵， ∴，

∴当时， ， 在上单调递减，

∵，∴.

∴当时， ，当时， ，

此时恰有三个零点.

当时， ，解得，

∴在上单调递减，在上单调递增，

∴，当时， ，此时不合题意；

当时， 恰有一个零点，此时符合题意；

当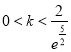时， ， ，

又∵，当时， .

∴在上有两个零点，此时在上有4个零点，不合题设.

综上， 的取值范围是.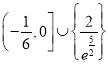

点晴:本题考查函数导数与单调性.确定零点的个数问题：可利用数形结合的办法判断交点个数，如果函数较为复杂，可结合导数知识确定极值点和单调区间从而确定其大致图象.方程的有解问题就是判断是否存在零点的问题，可参变分离，转化为求函数的值域问题处理. 恒成立问题以及可转化为恒成立问题的问题，往往可利用参变分离的方法，转化为求函数最值处理．也可构造新函数然后利用导数来求解.注意利用数形结合的数学思想方法.