题目内容
14．已知复数z的实部为-2，虚部为1，则$\overline{z}$的模等于$\sqrt{5}$．分析 通过复数z的实部为-2，虚部为1，可得$\overline{z}$=-2-i，进而可得结论．
解答 解：∵复数z的实部为-2，虚部为1，
∴z=-2+i，
∴$\overline{z}$=-2-i，
∴$|\overline{z}|$=$\sqrt{（-2）^{2}+（-1）^{2}}$=$\sqrt{5}$，
故答案为：$\sqrt{5}$．
点评 本题考查求复数的模，注意解题方法的积累，属于基础题．
练习册系列答案
相关题目
2．一个几何体的三视图如图所示，则其体积为（ ）
| A． | $\frac{4}{3}$（π+1） | B． | $\frac{2}{3}$（π+1） | C． | $\frac{4}{3}$（π+$\frac{1}{2}$） | D． | $\frac{2}{3}$（π+$\frac{1}{2}$） |
9．已知点A（-1，1），B（1，2），C（-2，-1），D（3，4），则向量$\overrightarrow{AB}$在$\overrightarrow{CD}$方向上的投影为（ ）
| A． | $-\frac{{3\sqrt{15}}}{2}$ | B． | $\frac{{3\sqrt{15}}}{2}$ | C． | $-\frac{{3\sqrt{2}}}{2}$ | D． | $\frac{{3\sqrt{2}}}{2}$ |
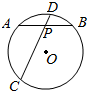如图，在半径为$\sqrt{7}$的⊙O中，弦AB、CD相交于点P，PA=PB=2，PD=1．