题目内容

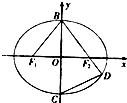
如图，在平面直角坐标系xOy中，F1，F2分别为椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点，B，C分别为椭圆的上、下顶点，直线BF2与椭圆的另一个交点为D，若cos∠F1BF2=
7
25
，则直线CD的斜率为______．
∵cos∠F1BF2=
7
25

∴2cos2∠OBF1-1=
7
25

∴cos∠OBF1=
4
5
即
b
a
=
4
5

∴e=
3
5
=
c
a

∵-
b2
a2
=kBD•kCD=-
b
c
•kCD，
∴kCD=
bc
a2
，
∴kCD=
bc
a2
=
12
25

故答案为：
12
25
练习册系列答案
相关题目
已知椭圆方程
x2
a2
+
y2
2a-1
=1(1＜a≤5)，过其右焦点做斜率不为0的直线l与椭圆交于A，B两点，设在A，B两点处的切线交于点M（x0，y0），则M点的横坐标x0的取值范围是（　　）
A．[4，+∞）B．[4，
25
4
]		C．(4，
25
4
]		D．(4，
25
4
)
椭圆E：
x2
a2
+y2=1的焦点在x轴上，且长轴长为短轴长的2倍，则它的离心率为（　　）
A．
1
2
B．
2
3
C．
3
2
D．
3
3
如下图，椭圆中心为O，F是焦点，A为顶点，准线l交OA延长线于B，P，Q在椭圆上且PD⊥l于D，QF⊥OA于F，则以下比值①
|PF|
|PD|
②
|QF|
|BF|
③
|AO|
|BO|
④
|AF|
|BA|
⑤
|FO|
|AO|
能作为椭圆的离心率的是______（填写所有正确的序号）
已知点P是椭圆
x2
16
+
y2
12
=1(y≠0)上的动点，F1，F2为椭圆的两个焦点，O是坐标原点，若M是∠F1PF2平分线上的一点，且F1M⊥MP，则OM的取值范围是______．
椭圆
x2
4
+
y2
3
=1内有一点P（1，-1），F为椭圆的右焦点，在椭圆上有一动点M，则|MP|+|MF|的取值范围为______．
已知F1，F2为椭圆
x2
25
+
y2
9
=1的两个焦点，A，B为过F1的直线与椭圆的两个交点，则△AF1F2的周长为______△ABF2周长为______．
设F1，F2分别为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点．
（1）设椭圆C上的点A(1，
3
2
)到两焦点的距离之和为4，求椭圆C的方程；
（2）设P是（1）中椭圆上的一点，∠F1PF2=60°求△F1PF2的面积．
在平面直角坐标系xOy中，已知椭圆
x2
4
+
y2
3
=1的左焦点为F，直线x-y-1=0，x-y+1=0与椭圆分别相交于点A，B，C，D，则AF+BF+CF+DF=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网