题目内容
已知函数 在
在 上单调递减,在(1,3)上单调递增在
上单调递减,在(1,3)上单调递增在 上单调递减,且函数图象在
上单调递减,且函数图象在 处的切线与直线
处的切线与直线 垂直.
垂直.
(Ⅰ)求实数 、
、 、
、 的值;(Ⅱ)设函数
的值;(Ⅱ)设函数 =0有三个不相等的实数根,求
=0有三个不相等的实数根,求 的取值范围.
的取值范围.
 在
在 上单调递减,在(1,3)上单调递增在
上单调递减,在(1,3)上单调递增在 上单调递减,且函数图象在
上单调递减,且函数图象在 处的切线与直线
处的切线与直线 垂直.
垂直.(Ⅰ)求实数
 、
、 、
、 的值;(Ⅱ)设函数
的值;(Ⅱ)设函数 =0有三个不相等的实数根,求
=0有三个不相等的实数根,求 的取值范围.
的取值范围.(Ⅰ)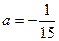 ,
,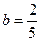 ,
,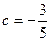 .(Ⅱ)
.(Ⅱ)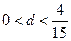
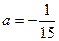 ,
,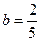 ,
,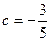 .(Ⅱ)
.(Ⅱ)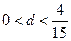
(Ⅰ)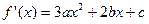 ,∵函数图象在
,∵函数图象在 处的切线与直线
处的切线与直线 垂直,∴
垂直,∴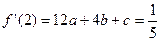 .①
.①
由已知可知,1和3为方程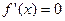 的两根,所以
的两根,所以
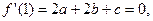 ②
②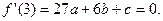 ③
③
由①、②、③解得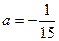 ,
,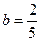 ,
,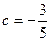 .…6分
.…6分
(Ⅱ)由(Ⅰ)得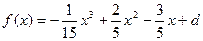 ,
,
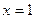 和
和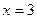 分别是函数
分别是函数 的极小值点和极大值点,且当
的极小值点和极大值点,且当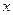 取负值且绝对值足够大时,
取负值且绝对值足够大时,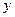 取正值,当
取正值,当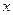 时正值且足够大时,
时正值且足够大时,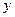 取负值.……8分
取负值.……8分
所以方程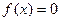 有三个不相等的实数根的充要条件为
有三个不相等的实数根的充要条件为
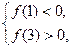 即
即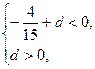 所以
所以 的取值范围为
的取值范围为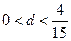 …12分
…12分
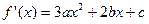 ,∵函数图象在
,∵函数图象在 处的切线与直线
处的切线与直线 垂直,∴
垂直,∴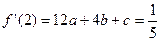 .①
.①由已知可知,1和3为方程
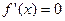 的两根,所以
的两根,所以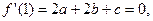 ②
②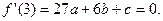 ③
③由①、②、③解得
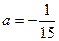 ,
,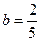 ,
,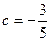 .…6分
.…6分(Ⅱ)由(Ⅰ)得
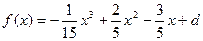 ,
,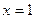 和
和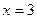 分别是函数
分别是函数 的极小值点和极大值点,且当
的极小值点和极大值点,且当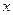 取负值且绝对值足够大时,
取负值且绝对值足够大时,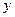 取正值,当
取正值,当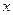 时正值且足够大时,
时正值且足够大时,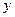 取负值.……8分
取负值.……8分所以方程
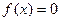 有三个不相等的实数根的充要条件为
有三个不相等的实数根的充要条件为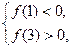 即
即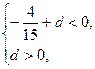 所以
所以 的取值范围为
的取值范围为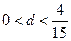 …12分
…12分
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
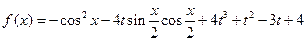 ,
,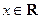 ,其中
,其中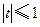 ,将
,将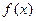 的最小值记为
的最小值记为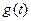 .
.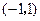 内的单调性并求极值.
内的单调性并求极值.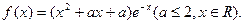
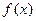 的单调区间
的单调区间

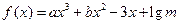 ,在
,在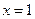 和
和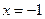 时取得极值,若对任意
时取得极值,若对任意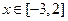 都有
都有 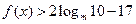 恒成立,求实数
恒成立,求实数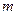 的取值集合.
的取值集合.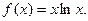 (Ⅰ)求函数
(Ⅰ)求函数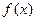 的单调区间和最小值;
的单调区间和最小值;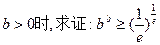 (其中e="2.718" 28…是自然对数的底数);
(其中e="2.718" 28…是自然对数的底数);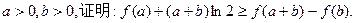
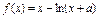 在
在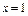 处取得极值。
处取得极值。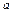 的值;(2)若关于
的值;(2)若关于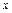 的方程
的方程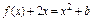 在
在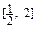 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数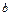 的取值范围;(3)证明:
的取值范围;(3)证明: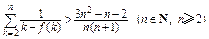 。参考数据:
。参考数据: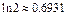 。
。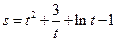 (t是时间,s是位移),则物体在时刻
(t是时间,s是位移),则物体在时刻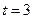 时的速度为 .
时的速度为 .