题目内容
13．三棱柱ABC-A1B1C1中，D是BC上的点，A1B∥面ADC1，D1为B1C1的中点．求证：面A1BD1∥面ADC1．分析 根据面面平行的判定定理即可得到结论．
解答 证明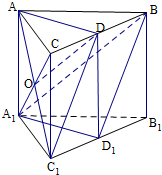
：∵在三棱柱ABC-A1B1C1中，D是BC上一点，
∴连结A1C，AC1交于O，连结OD，
∵A1B∥平面AC1D，
∴A1B∥OD，即D是BC的中点，
∵BD∥C1D1，且BD=C1D1，
∴四边形C1D1BD是平行四边形，
∴C1D∥BD1．
即BD1∥平面AC1D，
又∵A1B∩BD1=B，
∴平面A1BD1∥平面AC1D
点评 本题主要考查面面平行的判定，根据线面平行的性质定理得到D是BC的中点是解决本题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
3．已知等差数列{an}的公差d≠0，且a1，a5，a17依次成等比，则这个等比数列的公比是（ ）
| A． | $\frac{1}{2}$ | B． | 2 | C． | $\frac{1}{3}$ | D． | 3 |
8．下列命题中，真命题是（ ）
| A． | ?x0∈R，ex0≤0 | B． | a＞1，b＞1是ab＞1的充分条件 | ||
| C． | ?x∈R，2x＞x2 | D． | a+b=0的充要条件是$\frac{a}{b}$=-1 |