题目内容
3.已知函数f(x)=x2-2|x-a|(a∈R).(1)若函数f(x)为偶函数,求a的值
(2)当a>0时,若对任意的x∈[0,+∞),不等式f(x-1)≤2f(x)恒成立,求实数a的取值范围.
分析 (1)由偶函数的定义,化简整理,由恒成立思想可得a=0;
(2)由题意可得,x∈[0,+∞)时,不等式x2+2x-1+2|x-(a+1)|-4|x-a|≥0恒成立,再分①当0≤x≤a时、②当x≥a+1、③当a<x<a+1时三种情况,分别求得a的范围,再取交集,即为所求.
解答 解:(1)由函数y=f(x)为偶函数可知,
对任何x都有f(-x)=f(x),
得:(-x)2-2|-x-a|=x2-2|x-a|,
即|x+a|=|x-a|对任何x恒成立,
平方得:4ax=0对任何x恒成立,
而x不恒为0,则a=0;
(2)将不等式f(x-1)≤2f(x),
化为(x-1)2-2|x-1-a|≤2x2-4|x-a|,
即 4|x-a|-2|x-1-a|≤x2+2x-1(*)对任意x∈[0,+∞)恒成立,
①当0≤x≤a 时,将不等式(*)可化为 x2+4x+1-2a≥0,
对0≤x≤a上恒成立,则g(x)=x2+4x+1-2a 在(0,a]为单调递增,
只需g(x)min=g(0)=1-2a≥0,解得0<a≤$\frac{1}{2}$;
②当 a<x≤a+1时,将不等式(*)可化为x2-4x+1+6a≥0,
对a<x≤a+1上恒成立,由①可知0<a≤$\frac{1}{2}$,
则h(x)=x2-4x+1+6a 在(a,a+1]为单调递减,
只需h(x)min=h(a+1)=a2+4a-2≥0 得:a≤-$\sqrt{6}$-2或a≥$\sqrt{6}$-2,
即$\sqrt{6}$-2≤a≤$\frac{1}{2}$;
③当 x>a+1时,将不等式(*)可化为x2+2a-3≥0对x>a+1恒成立
则t(x)=x2+2a-3 在(a+1,+∞) 为单调递增,
由②可知$\sqrt{6}$-2≤a≤$\frac{1}{2}$都满足要求.
综上实数a的取值范围为:$\sqrt{6}$-2≤a≤$\frac{1}{2}$.
点评 本题主要考查分段函数的单调区间的求法和二次函数的性质的应用,体现了分类讨论、转化的数学思想,属于中档题

| A. | $\frac{a}{2}$ | B. | 1-$\frac{a}{2}$ | C. | 1-a | D. | $\frac{1-a}{2}$ |
| A. | 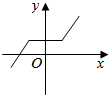 | B. | 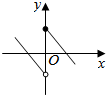 | C. |  | D. | 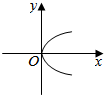 |
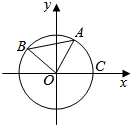 如图A、B是单位圆O上的动点,且A、B分别在第一、二象限,C是圆与x轴正半轴的交点,△AOB为正三角形,若A点的坐标为(x,y),计∠COA=α.
如图A、B是单位圆O上的动点,且A、B分别在第一、二象限,C是圆与x轴正半轴的交点,△AOB为正三角形,若A点的坐标为(x,y),计∠COA=α.