题目内容
【题目】已知数列{an}的前n项和为Sn , 且n+1=1+Sn对一切正整数n恒成立.
(1)试求当a1为何值时,数列{an}是等比数列,并求出它的通项公式;
(2)在(1)的条件下,当n为何值时,数列 ![]() 的前n项和Tn取得最大值.
的前n项和Tn取得最大值.
【答案】
(1)解:由an+1=1+Sn得:当n≥2时,an=1+Sn﹣1,
两式相减得:an+1=2an,
∵数列{an}是等比数列,∴a2=2a1,
又∵a2=1+S1=1+a1,解得:a1=1.
得: ![]()
(2)解: ![]() ,可知数列
,可知数列 ![]() 是一个递减数列,
是一个递减数列,
∴ ![]() ,
,
由此可知当n=9时,数列 ![]() 的前项和Tn取最大值
的前项和Tn取最大值
【解析】1、根据题意由an+1=1+Sn,推导出等比数列{an}的公比q=2,再根据等比数列的通项公式求得。
2、由题意可得数列 { l g ![]() } 是一个递减数列,根据题意可得前8项为正,故当n=9时数列的前项和Tn取最大值。
} 是一个递减数列,根据题意可得前8项为正,故当n=9时数列的前项和Tn取最大值。
【考点精析】掌握数列的前n项和是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系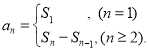 .
.

练习册系列答案
相关题目