题目内容
【题目】函数f(x)=ln|x﹣1|+2cosπx(﹣2≤x≤4)的所有零点之和等于( )
A.2
B.4
C.6
D.8
【答案】C
【解析】解:f(x)=ln|x﹣1|+2cosπx的零点,即为函数f(x)=﹣2cosπx与函数g(x)=ln|x﹣1|的图象交点的横坐标,
由图象变化的法则可知:y=ln|x﹣1|的图象作关于y轴的对称后和原来的一起构成y=ln|x|的图象,在向右平移1个单位得到y=ln|x﹣1|的图象
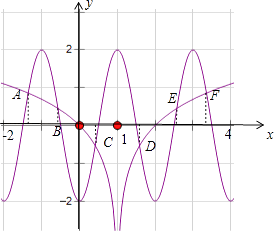
又f(x)=﹣2cosπx的周期为2,如图所示:两图象都关于直线x=1对称,且共有A,B,C,D,E,F,6个交点,
由中点坐标公式可得:xA+xF=2,xB+xE=2,xC+xD=2,故所有交点的横坐标之和为6,
所以答案是:C.
【考点精析】本题主要考查了函数的图象的相关知识点,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值才能正确解答此题.

练习册系列答案
相关题目